题目内容
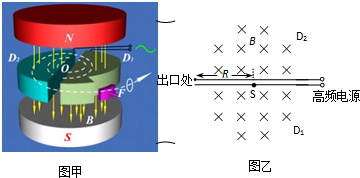
回旋加速器的工作原理如图所示，置于高真空中的D形金属盒半径为R，两盒间的狭缝很小，带电粒子穿过的时间可以忽略不计．磁感应强度为B的匀强磁场与盒面垂直．A处粒子源产生的粒子，质量为m、电荷量为+q，在加速器中被加速，加速电压为U．设粒子初速度为零，加速过程中不考虑相对论效应和重力作用（1）求粒子能获得的最大动能Ekm
（2）求粒子从静止开始加速到出口处所需的时间t．
分析：（1）当粒子从回旋加速器出来时，速度最大．根据qv B=m
求出最大速度，再根据EK=
mv2求出最大动能．
（2）粒子被电场加速一次动能的增加qU，根据最大动能求出加速的次数，粒子在磁场中运动一个周期被加速两次，从而知道粒子运动的周期次数，从而求出运动的时间．
| v2 |
| R |
| 1 |
| 2 |
（2）粒子被电场加速一次动能的增加qU，根据最大动能求出加速的次数，粒子在磁场中运动一个周期被加速两次，从而知道粒子运动的周期次数，从而求出运动的时间．
解答：解：（1）根据qv B=m
得，v=
则最大动能EKm=
mv2=
．
（2）粒子被电场加速一次动能的增加qU
则粒子被加速的次数n=
=
粒子在磁场中运动周期的次数n′=
=
T=
则粒子从静止开始到出口处所需的时间t=n′T=
?
=
．
| v2 |
| R |
| qBR |
| m |
则最大动能EKm=
| 1 |
| 2 |
| q2B2R2 |
| 2m |
（2）粒子被电场加速一次动能的增加qU
则粒子被加速的次数n=
| EK M |
| qU |
| qB2R2 |
| 2mU |
粒子在磁场中运动周期的次数n′=
| n |
| 2 |
| qB2R2 |
| 4mU |
T=
| 2πm |
| qB |
则粒子从静止开始到出口处所需的时间t=n′T=
| qB2R2 |
| 4mU |
| 2πm |
| qB |
| πBR2 |
| 2U |
点评：解决本题的关键知道粒子出回旋加速器时速度最大，根据qv B=m
可求出最大速度．以及知道粒子在磁场中运动的周期和交流电变化的周期相等．
| v2 |
| R |
练习册系列答案
相关题目
（2012?合肥三模）回旋加速器的工作原理如图所示，置于髙真空中的两个D形金属盒分别和高频交流电源 相连接，两盒间的狭缝很小，带电粒子穿过的时间可以忽略不计，匀强磁场与盒面垂直． A处粒子源产生的粒子（初速度和重力均忽略不计），在两盒之间被电场加速，直到达到 最大圆周半径时被引出．现用该装置分别加速质子和a粒子（a粒子电荷量是质子的2倍，a粒子质量是质 子的4倍），保持高频交流电源的频率不变，粒子在磁 场中做圆周运动的频率等于加速电场的频率，则质子 与a粒子最大动能之比为（ ）
1932年，美国的物理学家劳伦斯设计出了回旋加速器．回旋加速器的工作原理如图所示，置于高真空中的两D形金属盒半径为R，两盒间的狭缝很小，带电粒子穿过的时间可以忽略不计．磁感应强度为B的匀强磁场与盒面垂直．A处粒子源产生的质量为m、电荷量为+q粒子在加速器中被加速，其加速电压恒为U．带电粒子在加速过程中不考虑相对论效应和重力的作用．则（ ）
粒子回旋加速器的工作原理如图所示，置于真空中的D形金属盒的半径为R，两金属盒问的狭缝很小，磁感应强度为日的匀强磁场与金属盒盒面垂直，高频交流电的频率为厂，加速电压为U，若中心粒子源处产生的质子质量为m，电荷量为+e，在加速器中被加速．不考虑相对论效应，则下列说法正确是（ ）