题目内容
18.过去几千年来,人类对行星的认识与研究仅限于太阳系内,行星“51 peg b”的发现拉开了研究太阳系外行星的序幕,“51 peg b”绕其中心恒星做匀速圆周运动,周期约为4天,轨道半径约为地球绕太阳运动半径的$\frac{1}{20}$,该中心恒星与太阳的质量比约为( )| A. | $\frac{1}{10}$ | B. | 1 | C. | 5 | D. | 10 |
分析 研究行星绕某一恒星做匀速圆周运动,根据万有引力提供向心力,列出等式求出中心体的质量分析求解.
解答 解:研究行星绕某一恒星做匀速圆周运动,根据万有引力提供向心力,列出等式为:
$\frac{GMm}{{r}^{2}}$=m$\frac{{4π}^{2}}{{T}^{2}}$r
M=$\frac{{{4π}^{2}r}^{3}}{{GT}^{2}}$
“51 peg b”绕其中心恒星做匀速圆周运动,周期约为4天,轨道半径约为地球绕太阳运动半径的$\frac{1}{20}$,
所以该中心恒星与太阳的质量比约为$\frac{{(\frac{1}{20})}^{3}}{{(\frac{4}{365})}^{2}}$≈1,
故选:B.
点评 要求解一个物理量大小变化,我们应该把这个物理量先表示出来,再根据已知量进行判断.
向心力的公式选取要根据题目提供的已知物理量或所求解的物理量选取应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8. 一带有乒乓球发射机的乒乓球台如图所示,水平台面的长和宽分别为L1和L2,中间球网高度为h,发射机安装于台面左侧边缘的中点,能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为3h,不计空气的作用,重力加速度大小为g,若乒乓球的发射率v在某范围内,通过选择合适的方向,就能使乒乓球落到球网右侧台面上,到v的最大取值范围是( )
一带有乒乓球发射机的乒乓球台如图所示,水平台面的长和宽分别为L1和L2,中间球网高度为h,发射机安装于台面左侧边缘的中点,能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为3h,不计空气的作用,重力加速度大小为g,若乒乓球的发射率v在某范围内,通过选择合适的方向,就能使乒乓球落到球网右侧台面上,到v的最大取值范围是( )
 一带有乒乓球发射机的乒乓球台如图所示,水平台面的长和宽分别为L1和L2,中间球网高度为h,发射机安装于台面左侧边缘的中点,能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为3h,不计空气的作用,重力加速度大小为g,若乒乓球的发射率v在某范围内,通过选择合适的方向,就能使乒乓球落到球网右侧台面上,到v的最大取值范围是( )
一带有乒乓球发射机的乒乓球台如图所示,水平台面的长和宽分别为L1和L2,中间球网高度为h,发射机安装于台面左侧边缘的中点,能以不同速率向右侧不同方向水平发射乒乓球,发射点距台面高度为3h,不计空气的作用,重力加速度大小为g,若乒乓球的发射率v在某范围内,通过选择合适的方向,就能使乒乓球落到球网右侧台面上,到v的最大取值范围是( )| A. | $\frac{{L}_{1}}{2}$$\sqrt{\frac{g}{6h}}$<v<L1$\sqrt{\frac{g}{6h}}$ | B. | $\frac{{L}_{1}}{4}$$\sqrt{\frac{g}{h}}$<v<$\sqrt{\frac{(4{L}_{1}^{2}+{L}_{2}^{2})g}{6h}}$ | ||
| C. | $\frac{{L}_{1}}{2}$$\sqrt{\frac{g}{6h}}$<v<$\frac{1}{2}$$\sqrt{\frac{(4{L}_{1}^{2}+{L}_{2}^{2})g}{6h}}$ | D. | $\frac{{L}_{1}}{4}$$\sqrt{\frac{g}{h}}$<v<$\frac{1}{2}$$\sqrt{\frac{(4{L}_{1}^{2}+{L}_{2}^{2})g}{6h}}$ |
9.我国科学家正在研制航母舰载机使用的电磁弹射器,舰载机总质量为3.0×104kg,设起飞过程中发动机的推力恒为1.0×105N,弹射器有效作用长度为100m,推力恒定,要求舰载机在水平弹射结束时速度大小达到80m/s.弹射过程中舰载机所受总推力为弹射器和发动机推力之和,假设所受阻力为总推力的20%,则( )
| A. | 弹射器的推力大小为1.1×106N | |
| B. | 弹射器对舰载机所做的功为1.1×108J | |
| C. | 弹射器对舰载机做功的平均功率为8.8×107W | |
| D. | 舰载机在弹射过程中的加速度大小为32m/s2 |
13. 如图所示.是一个由电池、电阻R与平行班电容器组成的串联电路,在增大两极板间距离过程中( )
如图所示.是一个由电池、电阻R与平行班电容器组成的串联电路,在增大两极板间距离过程中( )
 如图所示.是一个由电池、电阻R与平行班电容器组成的串联电路,在增大两极板间距离过程中( )
如图所示.是一个由电池、电阻R与平行班电容器组成的串联电路,在增大两极板间距离过程中( )| A. | 电阻R中没有电流 | B. | 电容器的电容变小 | ||
| C. | 电阻R中有从a流向b的电流 | D. | 电容器储存的电能减小 |
10.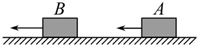 如图所示,A、B两小物块在光滑水平面上沿同一直线同向运动,动量分别为pA=6.0kg•m/s,pB=8.0kg•m/s.A追上B并与B相碰,碰后A、B的动量分别为pA′和pB′,pA′、pB′的值可能为( )
如图所示,A、B两小物块在光滑水平面上沿同一直线同向运动,动量分别为pA=6.0kg•m/s,pB=8.0kg•m/s.A追上B并与B相碰,碰后A、B的动量分别为pA′和pB′,pA′、pB′的值可能为( )
 如图所示,A、B两小物块在光滑水平面上沿同一直线同向运动,动量分别为pA=6.0kg•m/s,pB=8.0kg•m/s.A追上B并与B相碰,碰后A、B的动量分别为pA′和pB′,pA′、pB′的值可能为( )
如图所示,A、B两小物块在光滑水平面上沿同一直线同向运动,动量分别为pA=6.0kg•m/s,pB=8.0kg•m/s.A追上B并与B相碰,碰后A、B的动量分别为pA′和pB′,pA′、pB′的值可能为( )| A. | pA′=pB′=7.0kg•m/s | B. | pA′=3.0kg•m/s,pB′=11.0kg•m/s | ||
| C. | pA′=-2.0kg•m/s,pB′=16.0kg•m/s | D. | pA′=-6.0kg•m/s,pB′=20.0kg•m/s |
17.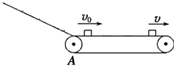 在工厂的流水线上安装有足够长的水平传送带,用水平传送带传送工件,可以大大提高工作效率,如图所示,水平传送带以恒定的速率v运送质量为m的工件,工件以v0(v0<v)的初速度从A位置滑上传送带,工件与传送带之间的动摩擦因数μ,已知重力加速度为g.( )
在工厂的流水线上安装有足够长的水平传送带,用水平传送带传送工件,可以大大提高工作效率,如图所示,水平传送带以恒定的速率v运送质量为m的工件,工件以v0(v0<v)的初速度从A位置滑上传送带,工件与传送带之间的动摩擦因数μ,已知重力加速度为g.( )
 在工厂的流水线上安装有足够长的水平传送带,用水平传送带传送工件,可以大大提高工作效率,如图所示,水平传送带以恒定的速率v运送质量为m的工件,工件以v0(v0<v)的初速度从A位置滑上传送带,工件与传送带之间的动摩擦因数μ,已知重力加速度为g.( )
在工厂的流水线上安装有足够长的水平传送带,用水平传送带传送工件,可以大大提高工作效率,如图所示,水平传送带以恒定的速率v运送质量为m的工件,工件以v0(v0<v)的初速度从A位置滑上传送带,工件与传送带之间的动摩擦因数μ,已知重力加速度为g.( )| A. | 工件滑上传送带到与传送带相对静止所需时间为$\frac{v-{v}_{0}}{g}$ | |
| B. | 因传送工件电动机多做的功为$\frac{1}{2}$m(v2-v02) | |
| C. | 传送带的摩擦力对工件所做的功为$\frac{1}{2}$m(v-v0)2 | |
| D. | 工件与传送带的相对位移为$\frac{(v-{v}_{0})^{2}}{2μg}$ |
 在倾斜角为θ的长斜面上,一带有风帆的滑块从静止开始沿斜面下滑,滑块(连同风帆)的质量为m,滑块与斜面间的动摩擦因数为μ,风帆受到的空气阻力与滑块下滑的速度v大小成正比,即f=kv(k未知),方向与v 的方向相反.滑块从静止开始沿斜面下滑的v-t图象如图所示,图中的倾斜直线是t=0时刻速度图线的切线.求:
在倾斜角为θ的长斜面上,一带有风帆的滑块从静止开始沿斜面下滑,滑块(连同风帆)的质量为m,滑块与斜面间的动摩擦因数为μ,风帆受到的空气阻力与滑块下滑的速度v大小成正比,即f=kv(k未知),方向与v 的方向相反.滑块从静止开始沿斜面下滑的v-t图象如图所示,图中的倾斜直线是t=0时刻速度图线的切线.求: