题目内容
1.据报道,我国自主研制的“嫦娥二号”探月飞行器环月飞行的高度距离月球表面100km,“嫦娥三号”探月飞行器落月制动前环月飞行的高度约为15km,若它们环月运行时均可视为圆周运动,则( )| A. | “嫦娥三号”环月运行的周期比“嫦娥二号”短 | |
| B. | “嫦娥三号”环月运行的速度比“嫦娥二号”小 | |
| C. | “嫦娥三号”环月运行时向心加速度比“嫦娥二号”大 | |
| D. | “嫦娥三号”环月运行时角速度比“嫦娥二号”小 |
分析 研究卫星绕地球做匀速圆周运动,根据万有引力提供向心力,列出等式表示出线速度、角速度、周期、加速度等物理量.
根据轨道半径的关系判断各物理量的大小关系.
解答 解:根据卫星做匀速圆周运动时万有引力提供向心力得:
F=$\frac{GMm}{{r}^{2}}$=m$\frac{{v}^{2}}{r}$=m$\frac{{4π}^{2}}{{T}^{2}}$r=mω2r=ma
A、周期T=2π$\sqrt{\frac{{r}^{3}}{GM}}$,“嫦娥二号”的轨道半径大于“嫦娥三号”的轨道半径,所以“嫦娥三号”环月运行的周期比“嫦娥二号”短,故A正确;
B、线速度v=$\sqrt{\frac{GM}{r}}$,“嫦娥二号”的轨道半径大于“嫦娥三号”的轨道半径,所以“嫦娥三号”环月运行的速度比“嫦娥二号”大,故B错误;
C、向心加速度a=$\frac{GM}{{r}^{2}}$,“嫦娥二号”的轨道半径大于“嫦娥三号”的轨道半径,所以“嫦娥三号”环月运行时向心加速度比“嫦娥二号”大,故C正确;
D、角速度ω=$\sqrt{\frac{GM}{{r}^{3}}}$,“嫦娥二号”的轨道半径大于“嫦娥三号”的轨道半径,所以“嫦娥三号”环月运行时角速度比“嫦娥二号”大,故D错误;
故选:AC.
点评 要比较一个物理量大小,我们应该把这个物理量先表示出来,在进行比较.向心力的公式选取要根据题目提供的已知物理量选取应用.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目
11.三种不同的入射光A、B、C分别射在三种不同的金属a、b、c表面,均恰能使金属中逸出光电子,若三种入射光的波长λA>λB>λC,则( )
| A. | 用入射光A照射金属b和c,金属b和c均可发出光电效应现象 | |
| B. | 用入射光A和B照射金属c,金属c可发生光电效应现象 | |
| C. | 用入射光C照射金属a与b,金属a、b均可发生光电效应现象 | |
| D. | 用入射光B和C照射金属a,使金属a不发生光电效应现象 |
9. 某同学将一直流电源的总功率PE、输出功率PR和电源内部的发热功率Pr随电流I变化的图线画在同一坐标系内,如图所示,根据图线可知( )
某同学将一直流电源的总功率PE、输出功率PR和电源内部的发热功率Pr随电流I变化的图线画在同一坐标系内,如图所示,根据图线可知( )
 某同学将一直流电源的总功率PE、输出功率PR和电源内部的发热功率Pr随电流I变化的图线画在同一坐标系内,如图所示,根据图线可知( )
某同学将一直流电源的总功率PE、输出功率PR和电源内部的发热功率Pr随电流I变化的图线画在同一坐标系内,如图所示,根据图线可知( )| A. | 反映Pr变化的图线是b | |
| B. | 电源电动势为8 V | |
| C. | 电源内阻为2Ω | |
| D. | 当电流为0.5 A时,外电路的电阻为6Ω |
16.如图为两分子系统的势能Ep与两分子间距离r的关系曲线.下列说法正确的是( )


| A. | 当r大于r1时,分子间的作用力表现为引力 | |
| B. | 当r小于r1时,分子间的作用力表现为斥力 | |
| C. | 当r等于r2时,分子间的作用力为零 | |
| D. | 在r由r1变到r2的过程中,分子间的作用力做正功 |

 如图所示,一列向右传播的简谐横波,波速大小为0.6m/s,P质点的横坐标x=0.96m,从图中状态开始计时,求:
如图所示,一列向右传播的简谐横波,波速大小为0.6m/s,P质点的横坐标x=0.96m,从图中状态开始计时,求:
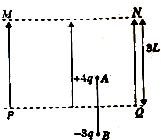 如图所示,在真空中的竖直平面内,用长为2L的绝缘轻杆连接两个质量均为m的带电小球A和B,A球的电荷量为+4q,B球的电荷量为-3q,组成一带电系统.虚线MN与PQ平行,开始时PQ恰为杆的中垂线.在MN与PQ间加竖直向上的匀强电场,恰能使带电系统静止不动.现使电场强度突然加倍(已知当地重力加速度为g),求:
如图所示,在真空中的竖直平面内,用长为2L的绝缘轻杆连接两个质量均为m的带电小球A和B,A球的电荷量为+4q,B球的电荷量为-3q,组成一带电系统.虚线MN与PQ平行,开始时PQ恰为杆的中垂线.在MN与PQ间加竖直向上的匀强电场,恰能使带电系统静止不动.现使电场强度突然加倍(已知当地重力加速度为g),求: