题目内容
4. 如图,MN是一个垂立纸面向里的匀强磁场的理想边界,现在其O点先后以初速v与MN成$\frac{π}{6}$角入射,质量均为m,带电路分别为+q和-q的带电微粒(不计重力).已知磁感强度为B,磁场区域足够大,则( )
如图,MN是一个垂立纸面向里的匀强磁场的理想边界,现在其O点先后以初速v与MN成$\frac{π}{6}$角入射,质量均为m,带电路分别为+q和-q的带电微粒(不计重力).已知磁感强度为B,磁场区域足够大,则( )| A. | 正负电荷在磁场中运动平均速度大小之比为1:1 | |
| B. | 正负电荷在磁场中运动平均速度大小之比为1:5 | |
| C. | 正负电荷在磁场中运动的时间之和为$\frac{2mπ}{qB}$ | |
| D. | 两粒子离开磁场的间距为$\frac{2mv}{qB}$ |
分析 由于正负粒子在磁场中的偏转方向相反,据左手定则,正粒子做逆时针、负粒子做顺时针方向的匀速圆周运动.先画出其运动轨迹,由几何关系和牛顿第二定律及运动学公式,求出正负粒子在磁场中的位移和时间中,从而也能求出粒子离开磁场时的间距.
解答 解:正负粒子在磁场中做匀速圆周运动的轨迹如图所示: 圆心分别为O和O′,由洛仑兹力提供向心力$qvB=\frac{m{v}^{2}}{r}$ 得到半径$r=\frac{mv}{qB}$,而运动周期$T=\frac{2πm}{qB}$,正粒子在磁场中偏转$\frac{5π}{3}$,负粒子在磁场中偏转$\frac{π}{3}$,由几何关系还可求出出射点与入射点的距离为$d=2rsin\frac{π}{6}=\frac{mv}{qB}$.
圆心分别为O和O′,由洛仑兹力提供向心力$qvB=\frac{m{v}^{2}}{r}$ 得到半径$r=\frac{mv}{qB}$,而运动周期$T=\frac{2πm}{qB}$,正粒子在磁场中偏转$\frac{5π}{3}$,负粒子在磁场中偏转$\frac{π}{3}$,由几何关系还可求出出射点与入射点的距离为$d=2rsin\frac{π}{6}=\frac{mv}{qB}$.
A、正粒子在磁场中的时间${t}_{1}=\frac{\frac{5π}{3}}{2π}T=\frac{5πm}{3qB}$,据平均速度的定义求得:正粒子的平均速度${v}_{1}=\frac{d}{{t}_{1}}=\frac{v}{5π}$ 负粒子在磁场中的运动时间${t}_{2}=\frac{2×\frac{π}{6}}{2π}T=\frac{πm}{3qB}$,负粒子的平均速度${v}_{2}=\frac{d}{{t}_{2}}=\frac{3v}{π}$,这样很容易求出$\frac{{v}_{1}}{{v}_{2}}=\frac{1}{5}$,所以A错.
B、由A选项中的结果知道$\frac{{v}_{1}}{{v}_{2}}=\frac{1}{5}$,所以B正确.
C、根据上述计算知道:${t}_{1}+{t}_{2}=\frac{2πm}{qB}=T$,所以C正确.
D、两粒子离开磁场的间距为$2d=\frac{2mv}{qB}$.
故选:BCD
点评 本题的关键是要画出正负粒子在磁场中的运动轨迹,由几何关系求出出射点离入射点的距离.由偏转角度求出粒子粒子在磁场中运动的时间,从而判断出正确结论.

 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案



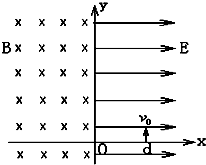 如图所示,在x>0的空间中,存在沿x轴方向的匀强电场,电场强度E=10N/C;在x<0的空间中,存在垂直xy平面方向的匀强磁场,磁感应强度B=0.5T.一带负电的粒子(比荷$\frac{q}{m}$=160C/kg,在x=0.06m处的d点以v0=8m/s的初速度沿y轴正方向开始运动,不计带电粒子的重力.求:
如图所示,在x>0的空间中,存在沿x轴方向的匀强电场,电场强度E=10N/C;在x<0的空间中,存在垂直xy平面方向的匀强磁场,磁感应强度B=0.5T.一带负电的粒子(比荷$\frac{q}{m}$=160C/kg,在x=0.06m处的d点以v0=8m/s的初速度沿y轴正方向开始运动,不计带电粒子的重力.求: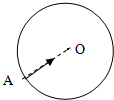 如图所示,一半径为R的绝缘圆筒中有沿轴线方向的匀强磁场,磁感应强度为B,一质量为m,带电量为q的正粒子(不计重力)以速度为v从筒壁的A孔沿半径方向进入筒内,设粒子与筒壁的碰撞无电量和能量的损失,那么要使粒子与筒壁连续碰撞,绕筒壁一周后恰好又从A孔射出,问:
如图所示,一半径为R的绝缘圆筒中有沿轴线方向的匀强磁场,磁感应强度为B,一质量为m,带电量为q的正粒子(不计重力)以速度为v从筒壁的A孔沿半径方向进入筒内,设粒子与筒壁的碰撞无电量和能量的损失,那么要使粒子与筒壁连续碰撞,绕筒壁一周后恰好又从A孔射出,问: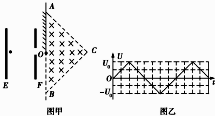 如图甲所示,在平行板电容器上加上如图乙所示的交变电压,在贴近E处有一粒子放射源,能够逐渐发射出大量质量为m,电荷量为q的带正电粒子,忽略粒子离开放射源时的初速度及粒子间的相互作用力,粒子只在电场力作用下运动,在电场中运动的时间极短可认为平行板间电压不变.从极板F射出的粒子能够继续沿直线向右运动,并由O点射入右侧的等腰直角三角形磁场区域.等腰直角三角形ABC的直角边边长为L.O为斜边AB的中点,在OA边上放有荧光屏,已知所有粒子刚好不能从AC边射出磁场,接收到粒子的荧光屏区域能够发光.求:
如图甲所示,在平行板电容器上加上如图乙所示的交变电压,在贴近E处有一粒子放射源,能够逐渐发射出大量质量为m,电荷量为q的带正电粒子,忽略粒子离开放射源时的初速度及粒子间的相互作用力,粒子只在电场力作用下运动,在电场中运动的时间极短可认为平行板间电压不变.从极板F射出的粒子能够继续沿直线向右运动,并由O点射入右侧的等腰直角三角形磁场区域.等腰直角三角形ABC的直角边边长为L.O为斜边AB的中点,在OA边上放有荧光屏,已知所有粒子刚好不能从AC边射出磁场,接收到粒子的荧光屏区域能够发光.求: 如图所示,在y轴左侧放置一加速电场和偏转电场构成的发射装置,C、D两板的中心线处于y=8cm的直线上;右侧圆形匀强磁场的磁感应强度大小为B=$\frac{2}{3}$T、方向垂直xoy平面向里,在x轴上方11cm处放置一个与x轴平行的光屏.已知A、B两板间电压UAB=100V,C、D两板间电压 UCD=300V,偏转电场极板长L=4cm,两板间距离d=6cm,磁场圆心坐标为(6,0)、半径R=3cm.现有带正电的某种粒子从A极板附近由静止开始经电场加速,穿过B板沿C、D两板间中心线y=8cm进入偏转电场,由y轴上某点射出偏转电场,经磁场偏转后打在屏上.带电粒子比荷$\frac{q}{m}$=106c/kg,不计带电粒子的重力.求:
如图所示,在y轴左侧放置一加速电场和偏转电场构成的发射装置,C、D两板的中心线处于y=8cm的直线上;右侧圆形匀强磁场的磁感应强度大小为B=$\frac{2}{3}$T、方向垂直xoy平面向里,在x轴上方11cm处放置一个与x轴平行的光屏.已知A、B两板间电压UAB=100V,C、D两板间电压 UCD=300V,偏转电场极板长L=4cm,两板间距离d=6cm,磁场圆心坐标为(6,0)、半径R=3cm.现有带正电的某种粒子从A极板附近由静止开始经电场加速,穿过B板沿C、D两板间中心线y=8cm进入偏转电场,由y轴上某点射出偏转电场,经磁场偏转后打在屏上.带电粒子比荷$\frac{q}{m}$=106c/kg,不计带电粒子的重力.求: 如图所示的直角坐标系中,在直线x=-2l0到y轴区域内存在着两个大小相等、方向相反的有界匀强电场,其中x轴上方的电场方向沿y轴负方向,x轴下方的电场方向沿y轴正方向.在电场左边界上A(-2l0,-l0)到C(-2l0,0)区域内,连续分布着电荷量为+q、质量为m的粒子.从某时刻起由A点到C点间的粒子,依次连续以相同的速度v0沿x轴正方向射入电场.若从A点射入的粒子,恰好从y轴上的A′(0,l0)沿x轴正方向射出电场,其轨迹如图虚线所示.不计粒子的重力及它们间的相互作用.求
如图所示的直角坐标系中,在直线x=-2l0到y轴区域内存在着两个大小相等、方向相反的有界匀强电场,其中x轴上方的电场方向沿y轴负方向,x轴下方的电场方向沿y轴正方向.在电场左边界上A(-2l0,-l0)到C(-2l0,0)区域内,连续分布着电荷量为+q、质量为m的粒子.从某时刻起由A点到C点间的粒子,依次连续以相同的速度v0沿x轴正方向射入电场.若从A点射入的粒子,恰好从y轴上的A′(0,l0)沿x轴正方向射出电场,其轨迹如图虚线所示.不计粒子的重力及它们间的相互作用.求 如图所示,MN、PQ是平行金属板,板长为L,两板间距离为$\frac{1}{2}$L,在PQ板的上方有垂直纸面向里的匀强磁场.一个电荷量为q、质量为m的带负电粒子以速度v0从MN板边缘沿平行于板的方向射入两板间,结果粒子恰好从PQ板左边缘飞进磁场,然后又恰好从PQ板的右边缘飞进电场.不计粒子重力.试求:
如图所示,MN、PQ是平行金属板,板长为L,两板间距离为$\frac{1}{2}$L,在PQ板的上方有垂直纸面向里的匀强磁场.一个电荷量为q、质量为m的带负电粒子以速度v0从MN板边缘沿平行于板的方向射入两板间,结果粒子恰好从PQ板左边缘飞进磁场,然后又恰好从PQ板的右边缘飞进电场.不计粒子重力.试求: