题目内容
13．如图所示，滑块由一理想弹簧发射器射出，经光滑轨道AB，光滑螺旋圆形BCDE和粗糙直轨道EF到达光滑平台FG，螺旋圆形BCDE的半径R=0.20m，平台FG的高度h=0.30m．轨道EF的长度s=0.8m．滑块与粗糙直轨道EF间的摩擦阻力Ff=0.1N，当弹簧压缩量为d时．能使质量m=0.05kg的滑块沿轨道上升到平台FG，并且滑块到达平台时的速度v=6m/s，滑块可视为质点，求：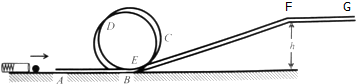
（1）滑块离开发射器到达平台FG的过程中重力对滑块做的功；
（2）滑块在粗糙直轨道上滑动过程中摩擦阻力对滑块做的功；
（3）当弹簧压缩量为d时弹簧的弹性势能；
（4）滑块能够完成整个过程到达平台FG，弹簧至少要多大的弹性势能．
分析 （1）滑块离开发射器到达平台FG的过程中重力对滑块做负功，根据上升的高度和重力求解；
（2）滑块在粗糙直轨道上滑动过程中，摩擦阻力对滑块做负功，且摩擦力是恒力，直接根据功的计算公式求解；
（3）对滑块运动的全过程，运用动能定理求弹力对滑块做功，由功能关系可得到弹簧压缩量为d时弹簧的弹性势能；
（4）滑块恰好到达圆形轨道最高点时，由重力提供向心力，由动能定理和功能关系求弹簧的弹性势能．
解答 解：（1）滑块离开发射器到达平台FG的过程中重力对滑块做的功为：WG=-mgh=-0.15J
（2）滑块在粗糙直轨道上滑动过程中摩擦阻力对滑块做的功为：Wf=-Ffs=-0.08J
（3）滑块运动的全过程，由动能定理得：W1+WG+Wf=$\frac{1}{2}m{v}^{2}$-0
代入数据解得：W1=1.13J
由功能关系可得，弹簧的弹性势能为1.13J．
（4）滑块能够到达最高点，由动能定理得：W2+W′G=$\frac{1}{2}m{v}_{1}^{2}$-0
在圆形最高点，有：mg=m$\frac{{v}_{1}^{2}}{R}$
解得：W2=0.25J
滑块克服粗糙轨道和平台高度，由动能定理有：
W3+W′G+Wf=0-0
解得：W3=0.23J
由于W2＞W3，所以弹簧弹性势能的最小值为0.25J．
答：（1）滑块离开发射器到达平台FG的过程中重力对滑块做的功是-0.15J；
（2）滑块在粗糙直轨道上滑动过程中摩擦阻力对滑块做的功是-0.08J；
（3）当弹簧压缩量为d时弹簧的弹性势能是 1.13J；
（4）滑块能够完成整个过程到达平台FG，弹簧至少要0.25J的弹性势能．
点评 解决本题的关键要选择解题过程，明确恒力做功的求法：功的计算公式，分段运用动能定理研究．
练习册系列答案
备战中考寒假系列答案
相关题目
3．
如图所示，边长为l的正方形线框abcd，电阻为R，处于磁感应强度为B的匀强磁场边缘，磁场方向垂直于纸面向外，线圈与磁感线垂直．在外力F将线圈以速度v向右匀速拉出磁场的过程中，则：（ ）
如图所示，边长为l的正方形线框abcd，电阻为R，处于磁感应强度为B的匀强磁场边缘，磁场方向垂直于纸面向外，线圈与磁感线垂直．在外力F将线圈以速度v向右匀速拉出磁场的过程中，则：（ ）| A． | 线圈产生的感应电流方向为a→d→c→b→a | |
| B． | 线圈产生的感应电动势大小为2Blv | |
| C． | 拉力F的大小为2$\frac{{B}^{2}{l}^{2}v}{R}$ | |
| D． | cd受到的安培力大小为：$\frac{{B}^{2}{l}^{2}v}{R}$ |
4．一辆质量为m，额定功率为P的小车从静止开始以恒定的加速度a起动，所受阻力为f，经时间t，行驶距离l后达到最大速度vm，然后匀速运动，则从静止开始到最大速度过程中，机车牵引力所做的功为（ ）
| A． | Pt | B． | （f+ma）l | C． | $\frac{1}{2}$mvm2 | D． | $\frac{1}{2}$mvm2+fl |
8．如图是某区域的电场线分布，A、B、C是电场中的三个点． 下列说法正确的是（ ）
| A． | A点的电场强度最强 | |
| B． | B点的电场强度最弱 | |
| C． | A、B、C三点的电场强度方向相同 | |
| D． | 正电荷、负电荷在B点受到的电场力方向相反 |
5．
如图所示为“割绳子”游戏中的一幅截图，游戏中割断左侧绳子糖果就会通过正下方第一颗星星，糖果一定能经过星星处吗？现将其中的物理问题抽象出来进行研究：三根不可伸长的轻绳共同系住一颗质量为m的糖果（可视为质点），设从左到右三根轻绳的长度分别为l1、l2和l3，其中最左侧的绳子处于竖直且张紧的状态，另两根绳均处于松弛状态，三根绳的上端分别固定在同一水平线上，且相邻两悬点间距离均为d，糖果正下方的第一颗星星与糖果距离为h．已知绳子由松弛到张紧时沿绳方向的速度分量即刻减为零，现将最左侧的绳子割断，以下选项正确的是（ ）
如图所示为“割绳子”游戏中的一幅截图，游戏中割断左侧绳子糖果就会通过正下方第一颗星星，糖果一定能经过星星处吗？现将其中的物理问题抽象出来进行研究：三根不可伸长的轻绳共同系住一颗质量为m的糖果（可视为质点），设从左到右三根轻绳的长度分别为l1、l2和l3，其中最左侧的绳子处于竖直且张紧的状态，另两根绳均处于松弛状态，三根绳的上端分别固定在同一水平线上，且相邻两悬点间距离均为d，糖果正下方的第一颗星星与糖果距离为h．已知绳子由松弛到张紧时沿绳方向的速度分量即刻减为零，现将最左侧的绳子割断，以下选项正确的是（ ）| A． | 只要满足l2≥$\sqrt{（{l}_{1}+h）^{2}+{d}^{2}}$，糖果就能经过正下方第一颗星星处 | |
| B． | 只要满足l3≥$\sqrt{（{l}_{1}+h）^{2}+4{d}^{2}}$，糖果就能经过正下方第一颗星星处 | |
| C． | 糖果可能以$\frac{mg{{l}_{2}}^{2}}{{d}^{2}}$（$\sqrt{{{l}_{2}}^{2}-{d}^{2}}$-l1）的初动能开始绕中间悬点做圆运动 | |
| D． | 糖果到达最低点的动能可能等于mg[l2-$\frac{（{{l}_{2}}^{2}-{d}^{2}）^{\frac{3}{2}}}{{{l}_{2}}^{2}}$-$\frac{{l}_{1}{d}^{2}}{{{l}_{2}}^{2}}$] |
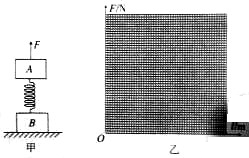质量均为4kg的物体A、B用一劲度系数k=200N/m的轻质弹簧连接，将它们竖直静止放在水平面上，如图甲所示，现将一竖直向上的变力F作用在A上，使A开始向上做匀加速运动，经0.40s物体B刚要离开地面．取g=10m/s2
物理学家在研究物理问题时，常常抓住问题的主要因素，忽略问题的次要因素，从而抽象出一个物理模型．比如，在高中阶段研究有关弹簧的问题时，由于弹簧本身质量很小，所以将弹簧抽象为质量不计的轻弹簧．为了探讨这种研究问题方法的可行性，我们以下面的问题为例进行探究．如图所示，水平光滑地面 上放有两个滑块A和B，质量分别为m和2m，其中B滑块上安装一只质量很小的轻弹簧，现给A一个初速度，大小为v0，则：