题目内容
如图所示，已知半径分别为R和r（R＞r）的甲、乙两个光滑的圆形轨道安置在同一竖直平面上，甲轨道左侧又连接一个光滑的轨道，两圆形轨道之间由一条水平轨道CD相连．一小球自某一高度由静止滑下，先滑上甲轨道，通过动摩擦因数为μ的CD段，又滑上乙轨道，最后离开圆轨道．若小球在两圆轨道的最高点对轨道压力都恰好为零．试求：（1）分别经过C、D时的速度；
（2）小球释放的高度h；
（3）水平CD段的长度．
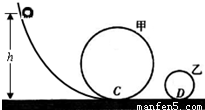
【答案】分析：小球滚到两圆轨道最高点均仅受重力，运用向心力公式可求出在其位置的速度．因为轨道光滑，则由机械能守恒定律可求出轨道最低点速度，从而也求出释放的高度．由于CD段粗糙，不能运用机械守恒定律，选用动能定理，就可算出长度，
解答：解：（1）小球在光滑圆轨道上滑行时，机械能守恒，设小球滑过C点时的速度为vc，通过甲环最高点速度为v′，根据小球对最高点压力为零，有
①
取轨道最低点为零势能点，由机械守恒定律
②
由①、②两式消去v′，可得
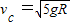③
同理可得小球滑过D点时的速度
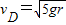④
所以小球经过C点的速度为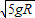
经过D点的速度为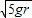
（2）小球从在甲轨道左侧光滑轨道滑至C点时机械能守恒，有
⑤
由③、⑤两式联立解得
h=2.5R
因此小球释放的高度为2.5R
（3）设CD段的长度为l，对小球滑过CD段过程应用动能定理
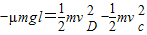⑥
由③、④、⑥三式联立解得
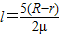
则有水平CD段的长度为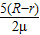
点评：掌握向心力公式外，还熟悉了牛顿第二定律，最后比较了机械能守恒定律与动能定理的优缺点．本题中小球在轨道最高点压力为零是解题的切入点．
解答：解：（1）小球在光滑圆轨道上滑行时，机械能守恒，设小球滑过C点时的速度为vc，通过甲环最高点速度为v′，根据小球对最高点压力为零，有
①取轨道最低点为零势能点，由机械守恒定律
②由①、②两式消去v′，可得
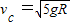③同理可得小球滑过D点时的速度
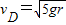④所以小球经过C点的速度为
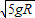经过D点的速度为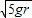（2）小球从在甲轨道左侧光滑轨道滑至C点时机械能守恒，有
⑤由③、⑤两式联立解得
h=2.5R
因此小球释放的高度为2.5R
（3）设CD段的长度为l，对小球滑过CD段过程应用动能定理
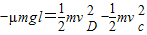⑥由③、④、⑥三式联立解得
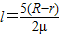
则有水平CD段的长度为
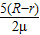
点评：掌握向心力公式外，还熟悉了牛顿第二定律，最后比较了机械能守恒定律与动能定理的优缺点．本题中小球在轨道最高点压力为零是解题的切入点．
练习册系列答案
名校课堂系列答案
相关题目
（2013?湛江一模）如图所示，两个质量相同的带电粒子以同一速度、同一位置由P点垂直于边界进入匀强磁场，在磁场中它们的运动轨迹如图所示．已知粒子a的运动轨道半径为r1，粒子b的运动轨迹半径为r2，且r2=2r1，q1、q2分别是粒子（ ）
2008年9月25日21时10分，神七飞船在酒泉卫星发射中心由长征二号F型火箭成功发射．飞船由火箭先送入近地点为A、远地点为B的椭圆轨道．26日4时03分，飞船在远地点启动变轨程序后，飞船进入预定圆轨道，如图所示．已知飞船在预定圆轨道上飞行n圈所用的时间为t，近地点距地面的高度为h1，地球表面的重力加速度为g，地球半径为R．求：
2007年10月24日18时29分，星箭成功分离之后，“嫦娥一号”卫星进入半径为205km的圆轨道上绕地球做圆周运动，卫星在这个轨道上“奔跑”一圈半后，于25日下午进行第一次变轨，变轨后，卫星轨道半径将抬高到离地球约600km的地方，如图所示．已知地球半径为R，表面重力加速度为g，求质量为m的“嫦娥一号”卫星以速率v在某一圆轨道上绕地球做圆周运动，求此时卫星距地球地面高度h1．
三颗人造卫星A、B、C环绕地球做匀速圆周运动，如图所示，已知mA=mC＜mB，A、B、C的轨道半径分别是RA，RB，RC，它们的周期分别是TA，TB，TC，则三颗卫星（ ）| A、B的线速度始终与C的线速度相同 | ||||||
| B、A的运行周期大于B的运行周期 | ||||||
| C、A的向心力大小大于C的向心力大小 | ||||||
D、半径与周期关系：
|
，OP=
R。求玻璃材料的折射率。