题目内容
15.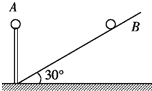 如图所示,A、B是带等量同种电荷的小球,A球固定在竖直放置的高为1m的绝缘支杆上,B静止于绝缘的倾角为30°的光滑斜面上时,恰与A等高.若已知B的质量为30$\sqrt{3}$ g,静电力常量k=9.0×109 N•m2/C2.则B带的电荷量是多少?(g取10m/s2)
如图所示,A、B是带等量同种电荷的小球,A球固定在竖直放置的高为1m的绝缘支杆上,B静止于绝缘的倾角为30°的光滑斜面上时,恰与A等高.若已知B的质量为30$\sqrt{3}$ g,静电力常量k=9.0×109 N•m2/C2.则B带的电荷量是多少?(g取10m/s2)
分析 对B球分析,B球受到重力、支持力与库仑力,且三力均不变.所以三力处于平衡状态.运用平衡条件列方程求解.
解答 解:设A、B所带电荷量均为Q,以B为对象,受力分析如右图,根据平衡条件
Ncos30°=mg
Nsin30°=F
$F=k\frac{{Q}^{2}}{(lcotθ)^{2}}$
联立以上三式得:
Q=$\sqrt{\frac{mg{l}^{2}cotθ}{k}}$=$\sqrt{\frac{30\sqrt{30}×1{0}^{-3}×10×{1}^{2}×\sqrt{3}}{9.0×1{0}^{9}}}$C=1.0×10-5 C
答:B所带的电荷量是1×10-5C.
点评 力平衡问题的解题一般按如下步骤进行:1、明确研究对象.2、分析研究对象受力,作出受力示意图.3、选择合适的方法,根据平衡条件列方程,求解.

练习册系列答案
相关题目
3.关于磁感线,下列说法正确的是( )
| A. | 磁感线是真实存在的,磁场中细铁屑排列的曲线就是磁感线 | |
| B. | 磁感线上每点的切线方向代表了该处的磁场方向 | |
| C. | 沿磁感线方向磁场逐渐减弱 | |
| D. | 磁场中的每条磁感线都不闭合 |
20. 如图所示,A、B为两个相同的双向力传感器,该型号传感器在受到拉力时示数为正,受到压力时示数为负.A连接质量不计的细绳,可沿固定的圆弧形轨道移动.B固定不动,通过光滑铰链连接长为0.3m的轻杆.将细绳连接在杆右端O点构成支架.始终保持杆水平,绳与杆的夹角∠AOB用θ表示.用另一绳在O点悬挂一个钩码,两个传感器的示数分别用F1、F2表示.移动传感器A改变θ,F1、F2的数值相应地发生变化,如表所示(g=10m/s2).则( )
如图所示,A、B为两个相同的双向力传感器,该型号传感器在受到拉力时示数为正,受到压力时示数为负.A连接质量不计的细绳,可沿固定的圆弧形轨道移动.B固定不动,通过光滑铰链连接长为0.3m的轻杆.将细绳连接在杆右端O点构成支架.始终保持杆水平,绳与杆的夹角∠AOB用θ表示.用另一绳在O点悬挂一个钩码,两个传感器的示数分别用F1、F2表示.移动传感器A改变θ,F1、F2的数值相应地发生变化,如表所示(g=10m/s2).则( )
 如图所示,A、B为两个相同的双向力传感器,该型号传感器在受到拉力时示数为正,受到压力时示数为负.A连接质量不计的细绳,可沿固定的圆弧形轨道移动.B固定不动,通过光滑铰链连接长为0.3m的轻杆.将细绳连接在杆右端O点构成支架.始终保持杆水平,绳与杆的夹角∠AOB用θ表示.用另一绳在O点悬挂一个钩码,两个传感器的示数分别用F1、F2表示.移动传感器A改变θ,F1、F2的数值相应地发生变化,如表所示(g=10m/s2).则( )
如图所示,A、B为两个相同的双向力传感器,该型号传感器在受到拉力时示数为正,受到压力时示数为负.A连接质量不计的细绳,可沿固定的圆弧形轨道移动.B固定不动,通过光滑铰链连接长为0.3m的轻杆.将细绳连接在杆右端O点构成支架.始终保持杆水平,绳与杆的夹角∠AOB用θ表示.用另一绳在O点悬挂一个钩码,两个传感器的示数分别用F1、F2表示.移动传感器A改变θ,F1、F2的数值相应地发生变化,如表所示(g=10m/s2).则( )| F1/N | 1.001 | 0.580 | … | 1.002 | … |
| F2/N | -0.868 | -0.291 | … | 0.865 | … |
| θ | 30° | 60° | … | 150° | … |
| A. | B传感器的示数对应的是表中力F1 | |
| B. | θ增大到90°前B传感器的示数一直减小 | |
| C. | 钩码质量为0.2 kg | |
| D. | θ=90°时传感器B的示数为0 |
7. 如图所示,带电荷量为-3Q与-Q的两点电荷分别固定在A、B两点,C、D两点将AB连线三等分.现使一个带正电荷的试探电荷从C点开始以某一初速度向右运动.则关于该电荷由C向D运动的过程,下列说法中可能正确的是( )
如图所示,带电荷量为-3Q与-Q的两点电荷分别固定在A、B两点,C、D两点将AB连线三等分.现使一个带正电荷的试探电荷从C点开始以某一初速度向右运动.则关于该电荷由C向D运动的过程,下列说法中可能正确的是( )
 如图所示,带电荷量为-3Q与-Q的两点电荷分别固定在A、B两点,C、D两点将AB连线三等分.现使一个带正电荷的试探电荷从C点开始以某一初速度向右运动.则关于该电荷由C向D运动的过程,下列说法中可能正确的是( )
如图所示,带电荷量为-3Q与-Q的两点电荷分别固定在A、B两点,C、D两点将AB连线三等分.现使一个带正电荷的试探电荷从C点开始以某一初速度向右运动.则关于该电荷由C向D运动的过程,下列说法中可能正确的是( )| A. | 一直做减速运动,且加速度逐渐减小 | |
| B. | 先做减速运动后做加速运动 | |
| C. | 一直做加速运动,且加速度逐渐减小 | |
| D. | 先做加速运动后做减速运动 |
4. 如图所示,某人用大小为F的恒力通过滑轮拉静止在水平面上的物体,开始时与物体相连的绳和水平面间的夹角为α,当拉力F作用一段时间后,绳与水平面间的夹角为β,物体获得的速度为v.已知滑轮上缘到物体的高度为h,绳和滑轮的质量不计,则( )
如图所示,某人用大小为F的恒力通过滑轮拉静止在水平面上的物体,开始时与物体相连的绳和水平面间的夹角为α,当拉力F作用一段时间后,绳与水平面间的夹角为β,物体获得的速度为v.已知滑轮上缘到物体的高度为h,绳和滑轮的质量不计,则( )
 如图所示,某人用大小为F的恒力通过滑轮拉静止在水平面上的物体,开始时与物体相连的绳和水平面间的夹角为α,当拉力F作用一段时间后,绳与水平面间的夹角为β,物体获得的速度为v.已知滑轮上缘到物体的高度为h,绳和滑轮的质量不计,则( )
如图所示,某人用大小为F的恒力通过滑轮拉静止在水平面上的物体,开始时与物体相连的绳和水平面间的夹角为α,当拉力F作用一段时间后,绳与水平面间的夹角为β,物体获得的速度为v.已知滑轮上缘到物体的高度为h,绳和滑轮的质量不计,则( )| A. | 拉力对物体做的功为Fh | |
| B. | 合外力对物体做的功为$\frac{1}{2}$mv2 | |
| C. | 阻力对物体做的功为Fh($\frac{1}{sinα}$-$\frac{1}{sinβ}$)-$\frac{1}{2}$mv2 | |
| D. | 物体的机械能的增加量为$\frac{1}{2}$mv2 |
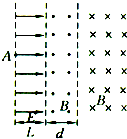 如图所示,空间分布着图示的匀强电场E(宽度为L和匀强磁场B(两部分磁场区域的磁感应强度大小相等、方向相反),一带正电的粒子质量为m,电荷量为q不计重力),从A点由静止释放经电场加速后进人磁场,穿过中间磁场进人右边磁场后能按某一路径而返回A点重复前述过程.求中间磁场的宽度d和粒子的运动周期.(虚线为磁场分界线,并不表示有什么障碍物)
如图所示,空间分布着图示的匀强电场E(宽度为L和匀强磁场B(两部分磁场区域的磁感应强度大小相等、方向相反),一带正电的粒子质量为m,电荷量为q不计重力),从A点由静止释放经电场加速后进人磁场,穿过中间磁场进人右边磁场后能按某一路径而返回A点重复前述过程.求中间磁场的宽度d和粒子的运动周期.(虚线为磁场分界线,并不表示有什么障碍物) 某学习小组探究“功与物体速度改变的关系”,设计了如下实验装置:在倾角可以调节的长斜面上安装两个速度传感器P、Q,其中Q固定、P可自由移动.让物体从斜面顶端下滑,并依次通过P、Q.
某学习小组探究“功与物体速度改变的关系”,设计了如下实验装置:在倾角可以调节的长斜面上安装两个速度传感器P、Q,其中Q固定、P可自由移动.让物体从斜面顶端下滑,并依次通过P、Q. 如图示是磁流体发电机的原理示意图.已知平行金属板A、B间距d=0.15m,其间有与极板平行的匀强磁场,磁感应强度的大小B=0.1T,等离子体以速度v=2×103m/s平行于极板从左侧垂直磁场射入.负载电阻R=5Ω.则
如图示是磁流体发电机的原理示意图.已知平行金属板A、B间距d=0.15m,其间有与极板平行的匀强磁场,磁感应强度的大小B=0.1T,等离子体以速度v=2×103m/s平行于极板从左侧垂直磁场射入.负载电阻R=5Ω.则 如图所示,在以坐标原点O为圆心、半径为R的圆形区域内,有相互垂直的匀强电场和匀强磁场,磁感应强度为B、方向垂直于xOy平面向里.一带正电的粒子(不计重力)从M点沿y轴正方向以某一速度射入,带电粒子恰好做匀速直线运动,经t0时间从N点射出.
如图所示,在以坐标原点O为圆心、半径为R的圆形区域内,有相互垂直的匀强电场和匀强磁场,磁感应强度为B、方向垂直于xOy平面向里.一带正电的粒子(不计重力)从M点沿y轴正方向以某一速度射入,带电粒子恰好做匀速直线运动,经t0时间从N点射出.