题目内容
10. 如图所示,质量为M的平板车P高h,质量为m的小物块Q的大小不计,位于平板车的左端,系统原来静止在光滑水平地面上.一不可伸长的轻质细绳长为R,一端悬于Q正上方高为R处,另一端系一质量也为m的小球(大小不计).今将小球拉至悬线与竖直位置成60°由静止释放,小球到达最低点时与Q的碰撞时间极短,且无机械能损失.已知Q离开平板车时速度大小是平板车速度的两倍,Q与P之间的动摩擦因数为μ,平板车与Q的质量关系是M:m=4:1,重力加速度为g.求:
如图所示,质量为M的平板车P高h,质量为m的小物块Q的大小不计,位于平板车的左端,系统原来静止在光滑水平地面上.一不可伸长的轻质细绳长为R,一端悬于Q正上方高为R处,另一端系一质量也为m的小球(大小不计).今将小球拉至悬线与竖直位置成60°由静止释放,小球到达最低点时与Q的碰撞时间极短,且无机械能损失.已知Q离开平板车时速度大小是平板车速度的两倍,Q与P之间的动摩擦因数为μ,平板车与Q的质量关系是M:m=4:1,重力加速度为g.求:(1)小物块Q离开平板车P时,P和Q的速度大小?
(2)平板车P的长度为多少?
(3)小物块Q落地时与平板车P的水平距离为多少?
分析 小球到达最低点时与Q的碰撞时间极短,且无能量损失,满足动量守恒的条件且能量守恒.小物块Q在平板车P上滑动的过程中,二者相互作用,动量守恒,部分动能转化为内能;同时注意平抛运动规律的正确应用.
解答 解:(1)设小球与Q碰前的速度为v0,小球下摆过程机械能守恒.
mgR(1-cos60°)=$\frac{1}{2}m{v_0}^2$①
由①式解得:v0=$\sqrt{gR}$②
小球与Q进行弹性碰撞,质量又相等,二者交换速度.
Q与P组成的系统,由动量守恒定律可得:
mv0=mv1+Mv2 ③
其中v2=$\frac{1}{2}{v_1}$,M=4m
将以上数据代入③式解得:v1=$\frac{{\sqrt{gR}}}{3}$,v2=$\frac{{\sqrt{gR}}}{6}$④
(2)对系统由能量守恒:$\frac{1}{2}m{v_0}^2$=$\frac{1}{2}m{v_1}^2$+$\frac{1}{2}M{v_2}^2$+μmgL ⑤
由⑤式解得:L=$\frac{7R}{18μ}$⑥
(3)Q脱离P后做平抛运动,由平抛运动规律可得:h=$\frac{1}{2}g{t^2}$⑦
由⑦式解得:t=$\sqrt{\frac{2h}{g}}$⑧
Q落地时二者相距:s=(v1-v2)t ⑨
由⑨式解得:s=$\frac{{\sqrt{2Rh}}}{6}$⑩
答:(1)小物块Q离开平板车P时,P和Q的速度大小为$\frac{{\sqrt{gR}}}{3}$、$\frac{{\sqrt{gR}}}{6}$;
(2)平板车P的长度为$\frac{7R}{18μ}$
(3)小物块Q落地时与平板车P的水平距离为$\frac{{\sqrt{2Rh}}}{6}$.
点评 逐一分析物体间的相互作用过程,分析得到物体间相互作用时满足的规律:动量守恒、能量守恒等,进而求出要求的物理量

 图示为某同学在做“研究匀变速直线运动”的实验时得到的一条纸带,A、B、C、D、E、F、G为相邻的7个计数点,每相邻两个计数点之间还有4个点没有画出.
图示为某同学在做“研究匀变速直线运动”的实验时得到的一条纸带,A、B、C、D、E、F、G为相邻的7个计数点,每相邻两个计数点之间还有4个点没有画出.(1)设电火花计时器的周期为T,则在打F点时的速度计算公式为vF=$\frac{{{d}_{6}-d}_{4}}{10T}$.(用字母表示)
(2)他经过测量并计算得到打点计时器在打B、C、D、E、F各点时物体的瞬时速度如表:
| 对应点 | B | C | D | E | F |
| 速度(m/s) | 0.141 | 0.180 | 0.221 | 0.260 | 0.302 |
| A. | 运行的速度都小于7.9km/s | B. | 所受的万有引力大小都相等 | ||
| C. | 都处于平衡状态 | D. | 离地面的高度都相同 |
| A. | 卢瑟福α粒子散射实验说明原子核内部具有复杂的结构 | |
| B. | 极限频率越大的金属材料逸出功越大 | |
| C. | 轻核聚变反应方程有:${\;}_{1}^{2}$H+${\;}_{1}^{3}$H→${\;}_{2}^{4}$He+${\;}_{0}^{1}$n | |
| D. | 氢原子从n=3能级跃迁到n=1能级和从n=2能级跃迁到n=1能级,前者跃迁辐射出的光子波长比后者的长 | |
| E. | 氦原子核由两个质子和两个中子组成,其中两个质子之间三种作用力从大到小的排列顺序为:核力、库仑力、万有引力 |
 实际电流表都有内阻,为了测量电流表G1的内阻rg,提供的器材如下:
实际电流表都有内阻,为了测量电流表G1的内阻rg,提供的器材如下: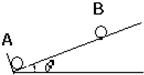 如图所示,带电小球A固定于足够长的光滑绝缘斜面的底端,另一带同种电荷的B小球从斜面某位置静止释放,在B沿斜面上滑到最高点的过程中,关于小球B的速度v、加速度a、电势能Ep、机械能E等四个物理量的大小随上滑位移x变化的图象可能正确的是( )
如图所示,带电小球A固定于足够长的光滑绝缘斜面的底端,另一带同种电荷的B小球从斜面某位置静止释放,在B沿斜面上滑到最高点的过程中,关于小球B的速度v、加速度a、电势能Ep、机械能E等四个物理量的大小随上滑位移x变化的图象可能正确的是( )




 如图所示,两根半径为r光滑的$\frac{1}{4}$圆弧轨道间距为L,电阻不计,在其上端连有一阻值为R0的电阻,整个装置处于竖直向上的匀强磁场中,磁感应强度为B.现有一根长度稍大于L、质量为m、电阻为R的金属棒从轨道的顶端PQ处开始下滑,到达轨道底端MN时对轨道的压力为2mg,求:
如图所示,两根半径为r光滑的$\frac{1}{4}$圆弧轨道间距为L,电阻不计,在其上端连有一阻值为R0的电阻,整个装置处于竖直向上的匀强磁场中,磁感应强度为B.现有一根长度稍大于L、质量为m、电阻为R的金属棒从轨道的顶端PQ处开始下滑,到达轨道底端MN时对轨道的压力为2mg,求: