题目内容
9. 如图,一个截面积为2S、盛有足够深的水的圆柱形容器放a在水平面上,容器内有一个活塞将水和一部分空气封闭,活塞能沿容器壁无摩擦滑动而不漏气.容器内水面上漂浮着一只倒扣的、薄壁圆柱形杯(杯的厚度可以忽略),其截面积为S,杯内封闭着一部分气体.当活塞与容器中杯外水面距离为H时,杯底与容器内的水面高度差为h,此时杯内气柱的高度为2h,压强与2h的水柱形成的压强相等.将活塞向下移动,使得杯底恰好与容器内的水面相平时,杯内、外水面高度均不变,杯内气柱的高度变为h,求活塞向下移动的距离x.(整个过程温度不变)
如图,一个截面积为2S、盛有足够深的水的圆柱形容器放a在水平面上,容器内有一个活塞将水和一部分空气封闭,活塞能沿容器壁无摩擦滑动而不漏气.容器内水面上漂浮着一只倒扣的、薄壁圆柱形杯(杯的厚度可以忽略),其截面积为S,杯内封闭着一部分气体.当活塞与容器中杯外水面距离为H时,杯底与容器内的水面高度差为h,此时杯内气柱的高度为2h,压强与2h的水柱形成的压强相等.将活塞向下移动,使得杯底恰好与容器内的水面相平时,杯内、外水面高度均不变,杯内气柱的高度变为h,求活塞向下移动的距离x.(整个过程温度不变)
分析 杯内的气体和容器中的气体温度不变,分别运用玻意耳定律列方程,即可求出活塞向下移动的距离.
解答 解:设杯外气体压强为${p}_{1}^{\;}$,杯内气体压强为${p}_{2}^{\;}$
${p}_{1}^{\;}+ρgh={p}_{2}^{\;}$①
根据题意有:${p}_{2}^{\;}=2ρgh$②
解得${p}_{1}^{\;}=ρgh$
对杯子,受力分析有:${p}_{2}^{\;}S=mg+{p}_{1}^{\;}S$③
联立得ρghS=mg
对杯子内外气体压力差不变,${p}_{1}^{′}+ρgh={p}_{2}^{′}$④
杯内气体体积变为原来的一半,根据玻意耳定律,有${p}_{2}^{\;}•2hS={p}_{2}^{′}hS$⑤
得${p}_{2}^{′}=2{p}_{2}^{\;}=4ρgh$⑥
${p}_{1}^{′}=3ρgh$=$3{p}_{1}^{\;}$⑦
对杯外气体,原来的压强为${p}_{1}^{\;}$
根据玻意耳定律知,体积为原来的$\frac{1}{3}$
原来体积H•2S-Sh
后来体积:(H-x)•2S
$(H-x)•2S=\frac{1}{3}(H•2S-Sh)$
解得:x=$\frac{4H+h}{6}$
答:活塞向下移动的距离x为$\frac{4H+h}{6}$
点评 本题考查玻意耳定律的应用和气体压强的计算,解题时要注意两部分气体压强之间的关系,结合一定的几何关系求体积.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.有一辆质量为800kg的小汽车驶上圆弧半径为50m的拱桥.汽车到达桥顶时速度为10m/s,汽车对桥的压力是6400N;汽车速度v=22.4 m/s时时恰好对桥没有压力而腾空.(g取10m/s2)
12.①验钞机的紫外线、②电视机遥控器的红外线、③CT机的X射线.它们都是电磁波,按频率高到低的排列顺序是( )
| A. | ①②③ | B. | ③②① | C. | ②③① | D. | ③①② |
17.一质量为m的物体,从距地面高度为h处由静止开始做自由落体运动则( )
| A. | 下落过程重力的平均功率为 mg$\sqrt{2gh}$ | B. | 下落过程重力的平均功率为$mg\frac{{\sqrt{2gh}}}{2}$ | ||
| C. | 落地时重力的瞬时功率为 mg$\sqrt{gh}$ | D. | 落地时重力的瞬时功率为 $\frac{1}{2}$mg$\sqrt{gh}$ |
4.A、B两小球在光滑水平面上沿同一直线向同一方向运动,A球的动量为5kg•m/s,B球的动量为7kg•m/s,当A球追上B球时发生对心碰撞,则碰撞后A、B两球动量的可能值为( )
| A. | pA′=6kg•m/s,pB′=8kg•m/s | B. | pA′=3kg•m/s,pB′=9kg•m/s | ||
| C. | pA′=-2kg•m/s,pB′=14kg•m/s | D. | pA′=-5kg•m/s,pB′=17kg•m/s |
14.火车在一段水平的直线轨道上匀加速运动,若阻力不变,则牵引力F和它的瞬时功率P的变化情况是( )
| A. | F不变,P变大 | B. | F变小,P不变 | C. | F变大,P变大 | D. | F不变,P不变 |
1. 如图所示为一交变电流随时间变化的图象,其中,从t=0开始的每个BIL-mg=ma时间内的图象均为半个周期的正弦曲线,则此交变电流的有效值为( )
如图所示为一交变电流随时间变化的图象,其中,从t=0开始的每个BIL-mg=ma时间内的图象均为半个周期的正弦曲线,则此交变电流的有效值为( )
 如图所示为一交变电流随时间变化的图象,其中,从t=0开始的每个BIL-mg=ma时间内的图象均为半个周期的正弦曲线,则此交变电流的有效值为( )
如图所示为一交变电流随时间变化的图象,其中,从t=0开始的每个BIL-mg=ma时间内的图象均为半个周期的正弦曲线,则此交变电流的有效值为( )| A. | $\sqrt{2}$A | B. | 3A | C. | $\frac{3}{2}$$\sqrt{5}$A | D. | 3$\sqrt{2}$A |
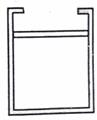 如图所示,开口处有卡口、内横截面积为S的圆柱形气缸,缸壁导热良好,气缸内总容积为V0,大气压强为P0,一厚度不计、质量为m(m=$\frac{0.2{P}_{0}S}{g}$)的活塞封闭住一定量的理想气体,温度为T0时缸内气体体积为0.8V0,活塞与气缸内壁间无摩擦.先在活塞上缓慢放上质量为2m的砂子,然后将缸内气体温度升高到2T0.气体的内能与热力学温度的关系是U=aT,其中a为常量.求:
如图所示,开口处有卡口、内横截面积为S的圆柱形气缸,缸壁导热良好,气缸内总容积为V0,大气压强为P0,一厚度不计、质量为m(m=$\frac{0.2{P}_{0}S}{g}$)的活塞封闭住一定量的理想气体,温度为T0时缸内气体体积为0.8V0,活塞与气缸内壁间无摩擦.先在活塞上缓慢放上质量为2m的砂子,然后将缸内气体温度升高到2T0.气体的内能与热力学温度的关系是U=aT,其中a为常量.求: