题目内容
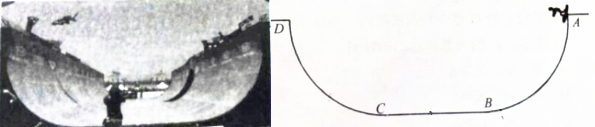
6. 一细杆与水桶相连,水桶中装有水,水桶与细杆一起在竖直平面内做圆周运动,如图所示,水的质量m=0.4kg,水的重心到转轴的距离l=40cm.取g=10m/s2,不计空气阻力.
一细杆与水桶相连,水桶中装有水,水桶与细杆一起在竖直平面内做圆周运动,如图所示,水的质量m=0.4kg,水的重心到转轴的距离l=40cm.取g=10m/s2,不计空气阻力.(1)若在最高点水不流出来,求桶的最小速率;
(2)若在最高点水桶的速率v=3m/s,求水对桶底的压力.
分析 (1)水桶运动到最高点时,水不流出恰好不流出时由水受到的重力刚好提供其做圆周运动的向心力,根据牛顿第二定律求解最小速率;
(2)水在最高点速率v=3m/s时,以水为研究对象,分析受力情况:重力和桶底的弹力,其合力提供水做圆周运动的向心力,由牛顿第二定律求解此弹力,再牛顿第三定律,水对桶的压力大小
解答 解:(1)以水桶中的水为研究对象,在最高点恰好不流出来,说明水的重力恰好提供其做圆周运动所需的向心力,此时桶的速率最小.此时有:
mg=m$\frac{{{v}_{min}}^{2}}{L}$
则所求的最小速率为:vmin=$\sqrt{gL}=\sqrt{10×0.4}$=2m/s
(2)设桶运动到最高点对水的弹力为F,则水受到重力和弹力提供向心力,根据牛顿第二定律,有:
mg+F=m$\frac{{v}^{2}}{L}$
解得:F=m$\frac{{v}^{2}}{L}$-mg=$\frac{9}{0.4}×0.4-0.4×10$=5N
根据牛顿第三定律,水对桶的压力大小:F′=F=5N
答:(1)若水桶转至最高点时水不流出来,水桶的最小速率为2m/s;
(2)若在最高点时水桶的速率 v=3m/s,水对桶底的压力大小为5N.
点评 本题应用牛顿第二定律破解水流星节目成功的奥秘,关键在于分析受力情况,确定向心力的来源.

练习册系列答案
相关题目
17.在物理学建立、发展的过程,许多物理学家的科学发现推动了人类历史的进步,关于科学家和他们的贡献,下列说法正确的是( )
| A. | 德国天文学家开普勒对他导师第谷观测的行星数据进行了多年研究,得出万有引力定律 | |
| B. | 英国物理学家卡文迪许利用“卡文迪许扭秤”首先较准确的测定了静电力常量 | |
| C. | 楞次发现了电磁感应现象,并研究提出了判断感应电流方向的方法--楞次定律 | |
| D. | 美国物理学家密立根经过多次实验,比较准确地测定了电子的电荷量 |
1.下面说法中正确的是( )
| A. | 加速度变化的运动必定是曲线运动 | |
| B. | 速度变化的运动必是曲线运动 | |
| C. | 加速度恒定的运动不可能是曲线运动 | |
| D. | 做曲线运动的物体的速度方向必变化 |
11. 一内壁光滑的细圆钢管,形状如图所示,一小钢球被一弹簧枪从A处正对着管口射入(射击时无机械能损失),欲使小钢球恰能到达C处及能从C点平抛恰好落回A点,在这两种情况下弹簧枪的弹性势能之比为( )
一内壁光滑的细圆钢管,形状如图所示,一小钢球被一弹簧枪从A处正对着管口射入(射击时无机械能损失),欲使小钢球恰能到达C处及能从C点平抛恰好落回A点,在这两种情况下弹簧枪的弹性势能之比为( )
 一内壁光滑的细圆钢管,形状如图所示,一小钢球被一弹簧枪从A处正对着管口射入(射击时无机械能损失),欲使小钢球恰能到达C处及能从C点平抛恰好落回A点,在这两种情况下弹簧枪的弹性势能之比为( )
一内壁光滑的细圆钢管,形状如图所示,一小钢球被一弹簧枪从A处正对着管口射入(射击时无机械能损失),欲使小钢球恰能到达C处及能从C点平抛恰好落回A点,在这两种情况下弹簧枪的弹性势能之比为( )| A. | 5:4 | B. | 2:3 | C. | 3:2 | D. | 4:5 |
18.泰山南天门前有一较长的阶梯,总共有几百级,某人先沿梯而上,然后又从原路返回到出发点,上去的平均速率为v1=0.6m/s,下来的平均速率为v2=3m/s,则往返全程的平均速度的大小和平均速率是( )
| A. | 1.8m/s,1.8m/s | B. | 1m/s,1m/s | C. | 0,1.8m/s | D. | 0,1m/s |
9.关于力对物体做功,下列说法中正确的是( )
| A. | 若物体所受合外力不为零,则合外力一定对物体做功 | |
| B. | 工人扛着行李在水平面上匀速前进时,工人对行李做正功 | |
| C. | 滑动摩擦力可以对物体做正功 | |
| D. | 对作用力与反作用力,若作用力做正功,则反作用力一定做负功 |
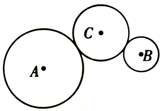 如图所示,摩擦轮A和B通过中介轮C进行传动,A为主动轮,B、C为从动轮,A的半径为20cm,B的半径为10cm,C的半径为15cm,则A、B两轮边缘上的点的线速度大小之比vA:vB=1:1,角速度之比ωA:ωB=1:2,向心加速度之比aA:aB=1:2.
如图所示,摩擦轮A和B通过中介轮C进行传动,A为主动轮,B、C为从动轮,A的半径为20cm,B的半径为10cm,C的半径为15cm,则A、B两轮边缘上的点的线速度大小之比vA:vB=1:1,角速度之比ωA:ωB=1:2,向心加速度之比aA:aB=1:2.