题目内容
13. 如图所示,在虚线范围内,用场强为E的匀强电场可使初速度为v0的某种正离子偏转θ角.在同样宽度范围内,若改用匀强磁场(方向垂直纸面向外),使该离子通过该区域并使偏转角度也为θ,则
如图所示,在虚线范围内,用场强为E的匀强电场可使初速度为v0的某种正离子偏转θ角.在同样宽度范围内,若改用匀强磁场(方向垂直纸面向外),使该离子通过该区域并使偏转角度也为θ,则(1)磁感应强度为多少?
(2)离子穿过电场和磁场的时间之比?
分析 (1)正离子在电场中做类平抛运动,水平方向做匀速直线运动,竖直方向做初速为零的匀加速直线运动,由牛顿第二定律和运动学公式结合得到偏转角正切tanθ的表达式.在磁场中,离子由洛伦兹力提供向心力,由几何知识求出半径,由牛顿第二定律求出sinθ.联立即可求得磁感应强度.
(2)离子穿过电场时,由水平方向的运动位移和速度求出时间.在磁场中,由t=$\frac{θ}{2π}$T求出时间,即可得解.
解答  解:(1)设粒子的质量m,电荷量q,场区宽度L,粒子在电场中做类平抛运动 $t=\frac{L}{v_0}$…①
解:(1)设粒子的质量m,电荷量q,场区宽度L,粒子在电场中做类平抛运动 $t=\frac{L}{v_0}$…①
$a=\frac{qE}{m}$…②
$tanθ=\frac{at}{V_0}$…③
由①②③得:$tanθ=\frac{{q{E}L}}{mv_0^2}$…④
粒子在磁场中做匀速圆周运动$R=\frac{{m{V_0}}}{qB}$…⑤
$sinθ=\frac{L}{R}$…⑥
由⑤⑥解得:$sinθ=\frac{qBL}{{m•{v_0}}}$…⑦
由④⑦式解得:$B=\frac{Ecosθ}{v_0}$
(2)粒子在电场中运动时间t1=$\frac{L}{{v}_{0}}$ ⑧
在磁场中运动时间 t2=$\frac{θm}{qB}$ ⑨
而L=$\frac{m{v}_{0}}{qB}sinθ$ ⑩
由⑧⑨⑩解出:$\frac{{t}_{1}}{{t}_{2}}$=$\frac{sinθ}{θ}$
答:(1)匀强磁场的磁感应强度是$\frac{Ecosθ}{{v}_{0}}$.
(2)离子穿过电场和磁场的时间之比是$\frac{sinθ}{θ}$.
点评 本题是离子分别在电场中和磁场中运动的问题,要抓住研究方法的区别:磁场中画出轨迹是常用的方法,电场中运动的合成与分解是基本方法,两种方法不能混淆.

 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案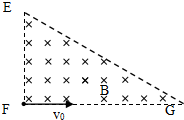 如图所示,匀强磁场的边界为直角三角形,∠EGF=30°,已知磁感应强度为B,方向垂直纸面向里.F处有一粒子源,沿FG方向发射出大量带正电荷q的同种粒子,粒子质量为m,粒子的初速度v0大小可调,则下列说法正确的是( )
如图所示,匀强磁场的边界为直角三角形,∠EGF=30°,已知磁感应强度为B,方向垂直纸面向里.F处有一粒子源,沿FG方向发射出大量带正电荷q的同种粒子,粒子质量为m,粒子的初速度v0大小可调,则下列说法正确的是( )| A. | 若粒子能到达EG边界,则粒子速度越大,从F运动到EG边的时间越长 | |
| B. | v0取合适值,粒子可以到达E点 | |
| C. | 能到达EF边界的所有粒子所用的时间均相等 | |
| D. | 粒子从F运动到EG边所用的最长时间为$\frac{5πm}{12qB}$ |
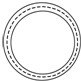 北京正负电子对撞机重大改造工程曾获中国十大科技殊荣,储存环是北京正负电子对撞机中非常关键的组成部分,如图为储存环装置示意图.现将质子(${\;}_{1}^{1}$H)和α粒子(${\;}_{2}^{4}$He)等带电粒子储存在储存环空腔中,储存环置于一个与圆环平面垂直的匀强磁场(偏转磁场)中,磁感应强度为B.如果质子和α粒子在空腔中做圆周运动的轨迹相同(如图中虚线所示),偏转磁场也相同.比较质子和α粒子在圆环状空腔中运动的动能EH和Eα,运动的周期TH和Tα的大小,有( )
北京正负电子对撞机重大改造工程曾获中国十大科技殊荣,储存环是北京正负电子对撞机中非常关键的组成部分,如图为储存环装置示意图.现将质子(${\;}_{1}^{1}$H)和α粒子(${\;}_{2}^{4}$He)等带电粒子储存在储存环空腔中,储存环置于一个与圆环平面垂直的匀强磁场(偏转磁场)中,磁感应强度为B.如果质子和α粒子在空腔中做圆周运动的轨迹相同(如图中虚线所示),偏转磁场也相同.比较质子和α粒子在圆环状空腔中运动的动能EH和Eα,运动的周期TH和Tα的大小,有( )| A. | EH=Eα,TH≠Tα | B. | EH=Eα,TH=Tα | C. | EH≠Eα,TH≠Tα | D. | EH≠Eα,TH=Tα |
| A. | U随R的增大而减小 | B. | 当R=0时,U=0 | ||
| C. | 当电路断开时,I=0,U=E | D. | 当R增大时,U也会增大 |
| A. | $\frac{s}{t_0}$ | B. | $\frac{{2(\sqrt{2}-1)s}}{t_0}$ | C. | $\frac{{2s(2-\sqrt{2})}}{t_0}$ | D. | $\frac{{s(2-\sqrt{2})}}{t_0}$ |
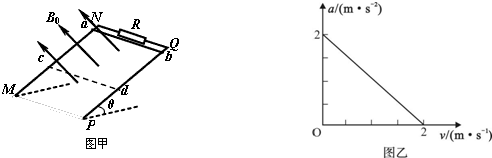 如图甲所示,MN、PQ为间距L=0.5m足够长的平行导轨,NQ⊥MN,导轨的电阻均不计.导轨平面与水平面间的夹角θ=37°,NQ间连接有一个R=4Ω的电阻.有一匀强磁场垂直于导轨平面且方向向上,磁感应强度为B0=1T,将一根质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上,且与导轨接触良好.现由静止释放金属棒,当金属棒滑行至cd处时达到稳定速度,已知在此过程中通过金属棒截面的电量q=0.2C,且金属棒的加速度a与速度v的关系如图乙所示,设金属棒沿导轨向下运动过程中始终与NQ平行.(取g=10m/s2,sin37°=0.6,cos37°=0.8)求:
如图甲所示,MN、PQ为间距L=0.5m足够长的平行导轨,NQ⊥MN,导轨的电阻均不计.导轨平面与水平面间的夹角θ=37°,NQ间连接有一个R=4Ω的电阻.有一匀强磁场垂直于导轨平面且方向向上,磁感应强度为B0=1T,将一根质量为m=0.05kg的金属棒ab紧靠NQ放置在导轨上,且与导轨接触良好.现由静止释放金属棒,当金属棒滑行至cd处时达到稳定速度,已知在此过程中通过金属棒截面的电量q=0.2C,且金属棒的加速度a与速度v的关系如图乙所示,设金属棒沿导轨向下运动过程中始终与NQ平行.(取g=10m/s2,sin37°=0.6,cos37°=0.8)求: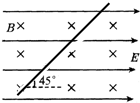 质量为m,带电量为q的微粒,以速度v与水平方向成45°角进入匀强电场和匀强磁场同时存在的空间(如图所示),微粒在电场、磁场、重力场的共同作用下做匀速直线运动,则带电粒子运动方向为沿轨迹向右上方,带电粒子带正电;电场强度大小为$\frac{mg}{q}$,磁感应强度的大小为$\frac{\sqrt{2}mg}{qv}$.
质量为m,带电量为q的微粒,以速度v与水平方向成45°角进入匀强电场和匀强磁场同时存在的空间(如图所示),微粒在电场、磁场、重力场的共同作用下做匀速直线运动,则带电粒子运动方向为沿轨迹向右上方,带电粒子带正电;电场强度大小为$\frac{mg}{q}$,磁感应强度的大小为$\frac{\sqrt{2}mg}{qv}$.

