题目内容
11. 在如图所示的正方形区域内有匀强磁场,一束电子以不同的速率从a点沿ab方向射入匀强磁场区域,最终又从磁场区域射出.则下列结论中正确的是( )
在如图所示的正方形区域内有匀强磁场,一束电子以不同的速率从a点沿ab方向射入匀强磁场区域,最终又从磁场区域射出.则下列结论中正确的是( )| A. | 从c点射出的电子和从d点射出的电子,其速率之比为2:1 | |
| B. | 从c点射出的电子和从d点射出的电子,其速率之比为1:2 | |
| C. | 若电子从bc边射出,则电子射入磁场时的速率越大,其在磁场中的运动时间就越长 | |
| D. | 若电子从ad边射出,则电子射入磁场时的速率越大,其在磁场中的运动时间就越短 |
分析 带电粒子在磁场中做圆周运动,由洛伦兹力提供向心力,先由几何知识可分别求得从c点和d点飞出的粒子的轨迹半径,则由牛顿第二定律和向心力公式求得两个粒子的速率,即可求出速率之比;由转动的角度可知运动时间之比.
解答 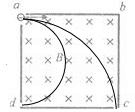 解:A、设电子在磁场中运动的轨迹半径为r,根据洛伦兹力提供向心力,得:qvB=m$\frac{{v}^{2}}{r}$,解得:v=$\frac{qBr}{m}$,可见,v∝r
解:A、设电子在磁场中运动的轨迹半径为r,根据洛伦兹力提供向心力,得:qvB=m$\frac{{v}^{2}}{r}$,解得:v=$\frac{qBr}{m}$,可见,v∝r
设磁场边长为L,如图所示,电子从c点离开磁场时,其轨迹半径为 rc=L;从d点离开磁场的电子,其轨迹半径为rd=$\frac{L}{2}$,
则得:vc:vd=2:l.故A正确,B错误.
C、由v=$\frac{qBr}{m}$可知,粒子在速度越大,粒子的轨道半径越大,若电子从bc边射出,则电子射入磁场时的速率越大,轨道半径越大,电子转过的圆心角越小,其在磁场中的运动时间就越短,故C错误;
D、若电子从ad边射出,则电子在磁场中转过的圆心角都相等,都是90°,它们在磁场中的运动时间相等,与电子的速率无关,故D错误;
故选:A.
点评 本题属于带电粒子在磁场中的偏转中典型题目,此类题的关键在于确定圆心及由几何关系求出半径.

练习册系列答案
 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
2.如图所示,在光滑水平面上放着两块长度相同,质量分别为M1和M2的木板,在两木板的左端各放一个大小、形状、质量完全相同的物块m,开始时,各物块均静止,今在两物块上各作用一水平恒力F1、F2,当物块和木板分离时,两木板的速度分别为v1和v2.物块和木板间的动摩擦因数相同.下列说法正确的是( )


| A. | 若F1=F2,M1>M2,则v1>v2 | B. | 若F1=F2,M1<M2,则v1<v2 | ||
| C. | 若 F1>F2,M1=M2,则v1>v2 | D. | 若F1<F2,M1=M2,则v1>v2 |
19.“探究加速度与力的关系”的实验装置如图甲.改变砂和砂桶质量,重新测出对应的加速度,多次测量后得到小车的加速度a和拉力F的数据如表(小车质量保持不变).

①根据表中的数据在图乙坐标图上作出a-F图象;
②由图象得到的实验结论是小车的质量不变时,小车的加速度与它所受的力成正比.
| F/N | 0.20 | 0.40 | 0.60 | 0.80 | 1.00 |
| a/(m•s-2) | 0.10 | 0.21 | 0.30 | 0.39 | 0.51 |

①根据表中的数据在图乙坐标图上作出a-F图象;
②由图象得到的实验结论是小车的质量不变时,小车的加速度与它所受的力成正比.
6.水平桌面上覆盖有玻璃板,玻璃板上放置一木块,下列说法正确的是( )
| A. | 木块受到的弹力是由于木块的弹性形变要恢复造成的,因为玻璃板没有形变 | |
| B. | 木块的重力就是木块对玻璃板的压力 | |
| C. | 木块对玻璃板的压力与玻璃板对木块的支持力是一对作用力与反作用力 | |
| D. | 木块对玻璃板的压力大小等于玻璃板对木块的支持力大小,因此二者合力为零 |
3. 如图所示,a、b灯分别标有“3.6V 4.0W”和“3.6V 2.5W”,闭合开关,调节R,能使a、b都正常发光.断开开关后重做实验,则( )
如图所示,a、b灯分别标有“3.6V 4.0W”和“3.6V 2.5W”,闭合开关,调节R,能使a、b都正常发光.断开开关后重做实验,则( )
 如图所示,a、b灯分别标有“3.6V 4.0W”和“3.6V 2.5W”,闭合开关,调节R,能使a、b都正常发光.断开开关后重做实验,则( )
如图所示,a、b灯分别标有“3.6V 4.0W”和“3.6V 2.5W”,闭合开关,调节R,能使a、b都正常发光.断开开关后重做实验,则( )| A. | 闭合开关,a将慢慢亮起来,b立即发光 | |
| B. | 闭合开关,a、b同时发光 | |
| C. | 闭合开关稳定时,a、b亮度相同 | |
| D. | 断开开关,a逐渐熄灭,b灯闪亮一下再熄灭 |
1.下列属于牛顿的主要贡献是( )
| A. | 发现光的色散 | B. | 创立相对论 | ||
| C. | 测出万有引力恒量 | D. | 发现摆的等时性 |
 如所示,质量为m的小球用长为L的不可伸长的轻质细线悬于O点,与O点处于同一水平线上的P点处有一根光滑的细钉,已知OP=$\frac{L}{2}$,要使小球能到达跟P点在同一竖直线的最高点B,求:
如所示,质量为m的小球用长为L的不可伸长的轻质细线悬于O点,与O点处于同一水平线上的P点处有一根光滑的细钉,已知OP=$\frac{L}{2}$,要使小球能到达跟P点在同一竖直线的最高点B,求: 两根足够长的光滑导轨竖直放置,间距L=2m,顶端接阻值R=9Ω的电阻.质量m=0.1kg、电阻r=lΩ的金属棒在磁场边界上方某处由静止释放,金属棒和导轨接触良好,磁感应强度B=IT的匀强磁场与导轨所在平面垂直,磁场足够大,如图所示,不计导轨电阻,重力加速度g=10m/s2.求:
两根足够长的光滑导轨竖直放置,间距L=2m,顶端接阻值R=9Ω的电阻.质量m=0.1kg、电阻r=lΩ的金属棒在磁场边界上方某处由静止释放,金属棒和导轨接触良好,磁感应强度B=IT的匀强磁场与导轨所在平面垂直,磁场足够大,如图所示,不计导轨电阻,重力加速度g=10m/s2.求: 在“验证机械能守恒定律”的实验中:
在“验证机械能守恒定律”的实验中: