题目内容
5.如图所示,装置的右边CD部分是长为L2=2m的水平面,一水平放置的轻质弹簧右端固定于D点并处于原长状态;装置的中间BC部分是长为L1=1m的水平传送带,它与左右两边的台面等高,并能平滑对接,传送带始终以v=3.5m/s的速度逆时针转动;装置的左边是一光滑的四分之一圆弧面,半径R=1.5m,圆心为O′,质量m=1kg的小滑块从A处由静止释放,到达O点时速度为零,OD间距x=0.4m,并且弹簧始终处在弹性限度内.已知滑块与传送带及右边水平面之间的动摩擦因数μ=0.25,取g=10m/s2.求
(1)滑块第一次到达C点时速度大小;
(2)弹簧储存的最大弹性势能;
(3)滑块再次回到左边曲面部分所能到达的最大高度.
分析 (1)滑块第一次从A到C的过程中,重力做功mgh,滑动摩擦力做功-μmgL1,根据动能定理求解滑块第一次到达C处的速度;
(2)滑块从C到O过程,其动能转化为内能和弹簧的弹性势能,由能量守恒定律求解弹簧储存的最大弹性势能;
(3)根据能量守恒定律求得滑块第二次经过C点时的速度大小,根据此速度与传送带速度的大小关系,判断出滑块将做匀加速运动,由运动学公式求出滑块的速度增加到与传送带相等时,通过的位移,即可知道滑块离开传送带时的速度.滑块从C到再次回到右边曲面部分所能到达的最大高度的过程中,重力做功,由动能定理求解最大高度.
解答 解:(1)设滑块第一次到达C处的速度为v1,对滑块从A到C的过程,根据动能定理得
mgh-μmgL1=$\frac{1}{2}m{v}_{1}^{2}$
解得,v1=$\sqrt{20}$m/s
(2)滑块从C到O过程,由能量守恒定律得
EP=$\frac{1}{2}m{v}_{1}^{2}$-μmg(L2-x)
解得,EP=2.75J
(3)设滑块再次到达C处的速度为v2,对滑块第一次到达C到再次到达C的过程,根据动能定理得
-2μmg(L2-x)=$\frac{1}{2}m{v}_{2}^{2}-\frac{1}{2}m{v}_{1}^{2}$,解得 v2=2m/s=v
可知,滑块接着相对传送带静止,速度为v=2m/s
对从B到最高点的过程,由动能定理得
-mgh′=0-$\frac{1}{2}m{v}^{2}$
解得,h′=0.2m
答:(1)滑块第一次到达B处的速度是$\sqrt{10}m/s$;
(2)弹簧储存的最大弹性势能是2.75J;
(3)滑块再次回到右边曲面部分所能到达的最大高度是0.2m.
点评 本题是多过程问题,分析滑块经历的过程,运用动能定理、牛顿第二定律和运动学公式结合按时间顺序分析和计算,难度适中.

实验步骤如下:

Ⅰ把轻弹簧一端固定在水平滑槽的左端,记录下弹簧自由端的位置O
Ⅱ放置物块M在某 C点处,记录下此C位置.用物块m压缩弹簧至某位置B处,记录下位置B,放手使物块m弹出,m和物块M碰撞后一起向右运动至停下,记录m和M碰后一起滑行的距离x
Ⅲ逐次在M上添加不同个数的砝码,重复几次Ⅱ,测出几个对应的x
已知m=20g,每个砝码的质量m0=5g,测量数据如表:
| 砝码数/个 | 0 | 1 | 2 | 3 | 4 |
| x(cm) | 100.00 | 44.40 | 25.00 | 16.01 | 11.10 |
| $\frac{1}{x}$(cm-1) | 0.010 | 0.023 | 0.040 | 0.063 | 0.090 |
| $\sqrt{x}$(cm0.5) | 10.00 | 6.70 | 5.00 | 4.00 | 3.30 |
| $\frac{1}{\sqrt{x}}$(cm-0.5) | 0.10 | 0.15 | 0.20 | 0.25 | 0.30 |
①每次实验都将M放在相同的C点,都让m压缩到相同的位置B再放手可以保正每次碰前m的速度相同(填“相同”或“不同”)
②若M在初始时按照图中的摆放方法,则测量x时,应测量C点到停下后M的右端(填“左端”或“右端”)间的距离
③利用碰撞后到停下的过程,可表示出碰后的速度为$\sqrt{2μgx}$(用g,x,μ表示)
④从表格中可以发现随着砝码个数增加,距离x变短,为找到定量规律,我们可以选用添加的砝码质量m1为纵坐标,$\frac{1}{\sqrt{x}}$(选填x、$\frac{1}{x}$、$\sqrt{x}$、$\frac{1}{\sqrt{x}}$)为横坐标,可做出如图2的直线函数图线.若延长得该直线的纵截距为-40g,则M的质量应为20g.
⑤利用③、④中的结论及表格中的任意一组数据,根据动量守恒定律,可以计算出m在碰前瞬间的速度.
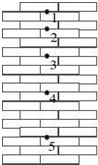 小球从竖直砖墙某位置由静止释放,用频闪照相机在同一底片上多次曝光,得到了图示的照片.已知连续两次曝光的时间间隔均为T,每块砖的厚度为d.根据图中信息,下列说法正确的是( )
小球从竖直砖墙某位置由静止释放,用频闪照相机在同一底片上多次曝光,得到了图示的照片.已知连续两次曝光的时间间隔均为T,每块砖的厚度为d.根据图中信息,下列说法正确的是( )| A. | 能判定位置“1”是小球释放的初始位置 | |
| B. | 能求出小球下落的加速度大小为a=$\frac{d}{4{T}^{2}}$ | |
| C. | 能求出小球在位置“3”的速度大小为V=$\frac{7d}{T}$ | |
| D. | 如果再知道当地的重力加速度,就可以验证小球下落过程中机械能是否守恒 |
| A. | 奔驰的骏马 | B. | 被踢出的足球 | ||
| C. | 从枪口飞出的子弹 | D. | 即将进入近地轨道的运载火箭 |
| A. | 行星绕太阳运动的开普勒常量k | |
| B. | 地球的公转周期,地球表面重力加速度 | |
| C. | 火星质量,火星半径,火星的公转周期 | |
| D. | 金星的公转轨道半径,金星的公转周期 |
| A. | 在空气中匀速下落的降落伞 | |
| B. | 沿光滑圆弧面下滑的小球 | |
| C. | 在空中做斜抛运动的铅球(不计空气阻力) | |
| D. | 物体以8m/S2加速下落 |
| A. | 保证小球飞出时的速度适当 | B. | 保证小球飞出时的初速度方向水平 | ||
| C. | 保证小球在空中的时间每次都相等 | D. | 保证小球的运动轨迹是一条抛物线 |
| A. | 布朗运动就是液体分子的运动,它说明了分子在永不停息地做无规则运动 | |
| B. | 密封在容积不变的容器内的气体,若温度升高,则气体分子对器壁单位面积上的平均作用力增大 | |
| C. | 第二类永动机违反了热力学第二定律,所以不可能制成 | |
| D. | 根据热力学第二定律可知,热量能够从高温物体传到低温物体,但不可能从低温物体传到高温物体 |