题目内容
15. 一个质量为m=4kg的物体静止在足够大的水平地面上,物体与地面间的动摩擦因数μ=0.1.从t=0开始,物体受到一个大小和方向呈周期性变化的水平力F作用,力F随时间的变化规律如图所示.则物体在12s时的速度为0,83s内物体的位移为112m.(g取10m/s2)
一个质量为m=4kg的物体静止在足够大的水平地面上,物体与地面间的动摩擦因数μ=0.1.从t=0开始,物体受到一个大小和方向呈周期性变化的水平力F作用,力F随时间的变化规律如图所示.则物体在12s时的速度为0,83s内物体的位移为112m.(g取10m/s2)
分析 首先要由图象求出来各个时间段内加速度大小,根据位移时间关系求解一个周期的位移,分析求得83秒内的总位移.
解答 解:当物体在0~2s内由牛顿第二定律,得:F1-μmg=ma1
解得:a1=$\frac{{F}_{1}-μmg}{m}$=$\frac{12-0.1×4×10}{4}m/{s}^{2}$=2m/s2,方向向前;
当物体在2s~4s内由牛顿第二定律,得:F2+μmg=ma2
a2=$\frac{{F}_{2}+μmg}{m}$=$\frac{4+0.1×4×10}{4}m/{s}^{2}$=2m/s2,方向向后;
所以在4s末时速度为零,4s~6s时间内物体静止;
故在一个周期结束时,物体速度为零.
则物体在12s时的速度为0;
则0~2s的位移为:x1=$\frac{1}{2}{a}_{1}{t}_{1}^{2}=\frac{1}{2}×2×4m=4m$,
后2~4s内的位移大小与0~2s内的位移大小相等,即:x2=4m;
4s末的速度为零;
4s~6s时间内拉力大小与摩擦力大小相等,位移为零;
所以一个周期的位移为x=x1+x2=8m,
83s有n=$\frac{83}{6}=13\frac{5}{6}$个周期,最后$\frac{5}{6}$个周期的时间为5s,此过程的位移也为8m;
83秒内物体的位移大小为:x=14×8m=112m.
故答案为:0;112m.
点评 本题涉及牛顿运动定律和运动学的知识以及运动定理的应用,求解本题的关键是认真分析物理过程,主要考查分析、推理和综合能力.

练习册系列答案
相关题目
6. 如图所示,b、c是匀强电场中距离相等的三个等势面,取等势面b的电势φb=0.一个带正电的粒子在等势面a以300eV的初动能沿垂直等势面方向向等势面c运动,到达等势面c时速度刚好为零.若带电粒子所受重力不计,在这个电场中,带电粒子的电势能为50eV时的动能是( )
如图所示,b、c是匀强电场中距离相等的三个等势面,取等势面b的电势φb=0.一个带正电的粒子在等势面a以300eV的初动能沿垂直等势面方向向等势面c运动,到达等势面c时速度刚好为零.若带电粒子所受重力不计,在这个电场中,带电粒子的电势能为50eV时的动能是( )
 如图所示,b、c是匀强电场中距离相等的三个等势面,取等势面b的电势φb=0.一个带正电的粒子在等势面a以300eV的初动能沿垂直等势面方向向等势面c运动,到达等势面c时速度刚好为零.若带电粒子所受重力不计,在这个电场中,带电粒子的电势能为50eV时的动能是( )
如图所示,b、c是匀强电场中距离相等的三个等势面,取等势面b的电势φb=0.一个带正电的粒子在等势面a以300eV的初动能沿垂直等势面方向向等势面c运动,到达等势面c时速度刚好为零.若带电粒子所受重力不计,在这个电场中,带电粒子的电势能为50eV时的动能是( )| A. | 200eV | B. | 150eV | C. | 100eV | D. | 50eV |
10. 一人乘电梯上楼,在竖直上升过程中加速度a随时间t变化的图线如图所示,以竖直向上为a的正方向,则下列说法中正确的是( )
一人乘电梯上楼,在竖直上升过程中加速度a随时间t变化的图线如图所示,以竖直向上为a的正方向,则下列说法中正确的是( )
 一人乘电梯上楼,在竖直上升过程中加速度a随时间t变化的图线如图所示,以竖直向上为a的正方向,则下列说法中正确的是( )
一人乘电梯上楼,在竖直上升过程中加速度a随时间t变化的图线如图所示,以竖直向上为a的正方向,则下列说法中正确的是( )| A. | t=2s时人对地板的压力最大 | B. | t=5s时人对地板的压力为0 | ||
| C. | t=8.5s时人对地板的压力最大 | D. | t=8.5s时人对地板的压力最小 |
5.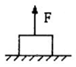 如图所示,一个重50N的物体置于光滑的水平面上,当用一个F=10N的力竖直向上拉物体时,物体所受的合力为( )
如图所示,一个重50N的物体置于光滑的水平面上,当用一个F=10N的力竖直向上拉物体时,物体所受的合力为( )
 如图所示,一个重50N的物体置于光滑的水平面上,当用一个F=10N的力竖直向上拉物体时,物体所受的合力为( )
如图所示,一个重50N的物体置于光滑的水平面上,当用一个F=10N的力竖直向上拉物体时,物体所受的合力为( )| A. | 0N | B. | 60N,方向竖直向上 | ||
| C. | 40N,方向竖直向上 | D. | 40N,方向竖直向下 |
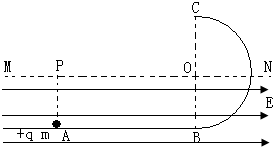 如图所示,粗糙水平轨道与半径为R的竖直光滑半圆轨道在B点平滑连接,在过圆心O的水平界面MN的下方分布有水平向右的匀强电场,场强E=$\frac{2mg}{q}$.现有一质量为m,电量为+q的小球(可视为质点)从水平轨道上A点由静止释放,小球运动到C点离开圆轨道后,经界面MN上的P点进入电场(P点恰好在A点的正上方).已知A、B间距离为2R,重力加速度为g,求:
如图所示,粗糙水平轨道与半径为R的竖直光滑半圆轨道在B点平滑连接,在过圆心O的水平界面MN的下方分布有水平向右的匀强电场,场强E=$\frac{2mg}{q}$.现有一质量为m,电量为+q的小球(可视为质点)从水平轨道上A点由静止释放,小球运动到C点离开圆轨道后,经界面MN上的P点进入电场(P点恰好在A点的正上方).已知A、B间距离为2R,重力加速度为g,求: 如图所示,一物体以初速度v0=5m/s 从上表面光滑的斜面底端滑上斜面.斜面的倾角为θ=300,则物体在斜面向上滑动的过程中的加速度大小为5 m/s2,加速度的方向为沿斜面向下,物体沿斜面能够上滑的最大距离为2.5 m.g=10m/s2.
如图所示,一物体以初速度v0=5m/s 从上表面光滑的斜面底端滑上斜面.斜面的倾角为θ=300,则物体在斜面向上滑动的过程中的加速度大小为5 m/s2,加速度的方向为沿斜面向下,物体沿斜面能够上滑的最大距离为2.5 m.g=10m/s2. 质谱仪是一种测定带电粒子质量和分析同位素的重要工具,其构造原理如图所示,离子源S产生质量为m,电量为q、初速为0的某种正离子,离子经过电压U加速后形成离子流,然后从S1处垂直于磁场进入矩形ABCD区域内的匀强磁场中,运动半周到达记录它的照相底片上的P点,已知P与S1的距离为x,离子形成的等效电流为I.求:
质谱仪是一种测定带电粒子质量和分析同位素的重要工具,其构造原理如图所示,离子源S产生质量为m,电量为q、初速为0的某种正离子,离子经过电压U加速后形成离子流,然后从S1处垂直于磁场进入矩形ABCD区域内的匀强磁场中,运动半周到达记录它的照相底片上的P点,已知P与S1的距离为x,离子形成的等效电流为I.求: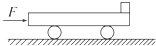 如图所示,质量M=8kg的小车放在光滑水平面上,在小车左端加一水平推力F=8N.当小车向右运动的速度达到3m/s时,在小车右端轻轻地放一个大小不计、质量
如图所示,质量M=8kg的小车放在光滑水平面上,在小车左端加一水平推力F=8N.当小车向右运动的速度达到3m/s时,在小车右端轻轻地放一个大小不计、质量