题目内容
14.在倾角为α的斜面上,一木块向上滑动,经t秒时间滑行L距离而停止,则木块与斜面间的动摩擦因数和木块再下滑至斜面底端所用的时间分别为( )| A. | $\frac{2L}{g{t}^{2}cosα}$-tanα,t$\sqrt{\frac{L}{g{t}^{2}sinα-L}}$ | B. | $\frac{Lcosα}{g{t}^{2}}$-tanα,t$\sqrt{\frac{gL}{{t}^{2}sinα-L}}$ | ||
| C. | $\frac{Lsinα}{{t}^{2}}$-cosα,t$\sqrt{\frac{gL}{{t}^{2}cosα-L}}$ | D. | $\frac{Ltanα}{g{t}^{2}}$-cosα,t$\sqrt{\frac{2gL}{g{t}^{2}-L}}$ |
分析 (1)将上滑匀减速直线运动视为反向的匀加速直线运动,根据位移时间关系知上滑加速度,根据牛顿运动定律求出小物块与斜面间的动摩擦因数.
(2)根据牛顿第二定律求出上滑的加速度,结合位移时间公式求出下滑的时间.
解答 解:(1)将上滑匀减速直线运动视为反向的匀加速直线运动,根据位移时间关系L=$\frac{1}{2}{a}_{1}{t}_{\;}^{2}$
知上滑加速度a1=$\frac{2L}{{t}^{2}}$
A沿斜面上滑,设与斜面间的动摩擦因数为μ,
由牛顿运动定律知,mgsinα+μmgcosα=ma1
解得μ=$\frac{2L}{g{t}^{2}cosα}$-tanα.
(2)A在斜面下滑,由牛顿运动定律知,mgsinα-μmgcosα=ma2
根据位移时间关系知L=$\frac{1}{2}$a2t${\;}_{2}^{2}$
解得t2=t$\sqrt{\frac{L}{g{t}^{2}sinα-L}}$.
故选:A
点评 本题考查了牛顿第二定律和运动学公式的综合,知道加速度是联系力学和运动学的桥梁,难度不大,注意计算即可.

练习册系列答案
相关题目
12. 如图所示,物体A、B叠放在一起,A用绳系在固定的墙上,用力F将B拉着右移,用T、fAB、fBA分别表示绳中拉力、A对B的摩擦力和B对A的摩擦力,则下面叙述中正确的是( )
如图所示,物体A、B叠放在一起,A用绳系在固定的墙上,用力F将B拉着右移,用T、fAB、fBA分别表示绳中拉力、A对B的摩擦力和B对A的摩擦力,则下面叙述中正确的是( )
 如图所示,物体A、B叠放在一起,A用绳系在固定的墙上,用力F将B拉着右移,用T、fAB、fBA分别表示绳中拉力、A对B的摩擦力和B对A的摩擦力,则下面叙述中正确的是( )
如图所示,物体A、B叠放在一起,A用绳系在固定的墙上,用力F将B拉着右移,用T、fAB、fBA分别表示绳中拉力、A对B的摩擦力和B对A的摩擦力,则下面叙述中正确的是( )| A. | F做正功,fAB做负功,fBA做正功,T不做功 | |
| B. | F做正功,fAB做负功,fBA和T不做功 | |
| C. | F、fBA做正功,fAB、T不做功 | |
| D. | F做正功,其他力都不做功 |
5.2014年5月10日天文爱好者迎来了“土星冲日”的美丽天象.“土星冲日”是指土星和太阳正好分处地球的两侧,三者几乎成一条直线.若土星和地球绕太阳公转的方向相同,公转轨迹都近似为圆.设土星公转周期为T1,公转半径为R1;地球公转周期为T2,公转半径为R2,万有引力常量为G.忽略土星与地球之间的引力作用,从发生“土星冲日”天象开始计时,下列说法正确的是( )
| A. | 土星公转速度大于地球公转速度 | |
| B. | 地球与土星相距最近经历的时间至少为$\frac{{T}_{1}{T}_{2}}{{T}_{1}-{T}_{2}}$ | |
| C. | 太阳的质量为$\frac{4{π}^{2}{{R}_{1}}^{3}}{G{{T}_{2}}^{2}}$ | |
| D. | 土星与地球公转的向心加速度之比为$\frac{{R}_{1}^{2}}{{R}_{2}^{2}}$ |
2. 如图所示,在匀强磁场中固定放置一根串接一电阻R的直角形金属导轨aob(在纸面内),磁场方向垂直纸面朝里,另有两根金属导轨c、d分别平行于oa、ob放置围成图示的一个正方形回路.保持导轨之间接触良好,金属导轨的电阻不计.现经历以下两个过程:①以速率v移动d,使它与ob的距离增大一倍;②再以同样速率v移动c,使它与oa的距离减小一半;设上述两个过程中电阻R产生的热量依次为Q1、Q2,则( )
如图所示,在匀强磁场中固定放置一根串接一电阻R的直角形金属导轨aob(在纸面内),磁场方向垂直纸面朝里,另有两根金属导轨c、d分别平行于oa、ob放置围成图示的一个正方形回路.保持导轨之间接触良好,金属导轨的电阻不计.现经历以下两个过程:①以速率v移动d,使它与ob的距离增大一倍;②再以同样速率v移动c,使它与oa的距离减小一半;设上述两个过程中电阻R产生的热量依次为Q1、Q2,则( )
 如图所示,在匀强磁场中固定放置一根串接一电阻R的直角形金属导轨aob(在纸面内),磁场方向垂直纸面朝里,另有两根金属导轨c、d分别平行于oa、ob放置围成图示的一个正方形回路.保持导轨之间接触良好,金属导轨的电阻不计.现经历以下两个过程:①以速率v移动d,使它与ob的距离增大一倍;②再以同样速率v移动c,使它与oa的距离减小一半;设上述两个过程中电阻R产生的热量依次为Q1、Q2,则( )
如图所示,在匀强磁场中固定放置一根串接一电阻R的直角形金属导轨aob(在纸面内),磁场方向垂直纸面朝里,另有两根金属导轨c、d分别平行于oa、ob放置围成图示的一个正方形回路.保持导轨之间接触良好,金属导轨的电阻不计.现经历以下两个过程:①以速率v移动d,使它与ob的距离增大一倍;②再以同样速率v移动c,使它与oa的距离减小一半;设上述两个过程中电阻R产生的热量依次为Q1、Q2,则( )| A. | Q1=Q2 | B. | Q1=2Q2 | C. | Q2=2Q1 | D. | Q2=4Q1 |
3.宇宙中存在着这样一种四星系统,这四颗星的质量相等,远离其他恒星,因此可以忽略其他恒星对它们的作用,四颗星稳定地分布在一个正方形的四个顶点上,且均围绕正方形对角线的交点做匀速圆周运动,假设每颗星的质量为m,正方形的边长为L,每颗星的半径为R,引力常量为G,则( )
| A. | 每颗星做圆周运动的半径为$\frac{1}{2}$L | |
| B. | 每颗星做圆周运动的向心力为$\frac{{({1+\sqrt{2}})G{m^2}}}{{2{L^2}}}$ | |
| C. | 每颗星表面的重力加速度为$\frac{Gm}{R^2}$ | |
| D. | 每颗星做圆周运动的周期为$2π\sqrt{\frac{{\sqrt{2}{L^3}}}{{(1+2\sqrt{2})Gm}}}$ |


 质谱仪又称质谱计,是分离和检测不同同位素的仪器.如图所示为质谱仪的工作原理简化示意图.现利用这种质谱仪对某元素进行测量,已知该元素的两种同位素(电量相同,质量不同)的质量之比为1:2,不计重力,它们从容器A右方的小孔S无初速飘入
质谱仪又称质谱计,是分离和检测不同同位素的仪器.如图所示为质谱仪的工作原理简化示意图.现利用这种质谱仪对某元素进行测量,已知该元素的两种同位素(电量相同,质量不同)的质量之比为1:2,不计重力,它们从容器A右方的小孔S无初速飘入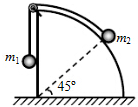 如图所示,水平面上固定一四分之一的球体,球体左侧面光滑,质量分别为m1和m2的小物块(可视为质点)通过柔软光滑的软绳连接后静止于球面上,此时m2与球心O的连线与水平方向成45°,m2与球面间的动摩擦因数为0.5,设m2与球面之间的最大静摩擦力等于滑动摩擦力,则$\frac{{m}_{1}}{{m}_{2}}$可能为( )
如图所示,水平面上固定一四分之一的球体,球体左侧面光滑,质量分别为m1和m2的小物块(可视为质点)通过柔软光滑的软绳连接后静止于球面上,此时m2与球心O的连线与水平方向成45°,m2与球面间的动摩擦因数为0.5,设m2与球面之间的最大静摩擦力等于滑动摩擦力,则$\frac{{m}_{1}}{{m}_{2}}$可能为( )