��Ŀ����
2�� ��ͼ��ʾ������ǿ�ų��й̶�����һ������һ����R��ֱ���ν�������aob����ֽ���ڣ����ų�����ֱֽ�泯�����������������c��d�ֱ�ƽ����oa��ob����Χ��ͼʾ��һ�������λ�·�����ֵ���֮��Ӵ����ã���������ĵ��費�ƣ��־��������������̣���������v�ƶ�d��ʹ����ob�ľ�������һ����������ͬ������v�ƶ�c��ʹ����oa�ľ����Сһ�룻���������������е���R��������������ΪQ1��Q2��������
��ͼ��ʾ������ǿ�ų��й̶�����һ������һ����R��ֱ���ν�������aob����ֽ���ڣ����ų�����ֱֽ�泯�����������������c��d�ֱ�ƽ����oa��ob����Χ��ͼʾ��һ�������λ�·�����ֵ���֮��Ӵ����ã���������ĵ��費�ƣ��־��������������̣���������v�ƶ�d��ʹ����ob�ľ�������һ����������ͬ������v�ƶ�c��ʹ����oa�ľ����Сһ�룻���������������е���R��������������ΪQ1��Q2��������| A�� | Q1=Q2 | B�� | Q1=2Q2 | C�� | Q2=2Q1 | D�� | Q2=4Q1 |
���� ��������c��d�����ƶ������ݸ�Ӧ�綯�ơ�ŷķ���ɵ��г�������������ʽ���о���ϵ��
��� �⣺��d��ob֮�����Ϊl1��c��oa֮�����Ϊl2��
��Q1=I1t1=$\frac{B{l}_{2}v}{R}$•$\frac{{l}_{1}}{v}$=$\frac{B{l}_{1}{l}_{2}}{R}$
Q2=I2t2=$\frac{B•2{l}_{1}v}{R}$•$\frac{\frac{{l}_{2}}{2}}{v}$=$\frac{B{l}_{1}{l}_{2}}{R}$
��Q1=Q2����A��ȷ��BCD����
��ѡ��A��
���� ����ķ������ĸ�����������ͬ������ʾ��Ҳ�����þ��鹫ʽ��Ӧ����q=n$\frac{����}{R}$��������ͨ���仯��С��ȷ����

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
20�����������з�������ѧʷʵ���У�������
| A�� | �²����������ʵ������Ҳ���в����� | |
| B�� | ����ͨ��������ɢ��ʵ�飬�����ԭ�ӵĺ�ʽ�ṹѧ˵ | |
| C�� | ��ķ������������ | |
| D�� | ��������ȷ�������Ȼ�������� |
10�� ��ͼ��ʾ�ĵ�·��R1Ϊ�������裨����ֵ�����ܹ���ǿ�ȵ��������С�����þ�Եϸ�߰�һ����С����Ϊ���ɣ�ϵ��ƽ�а�������Ľ�����A���ڲ���森��R2�Ļ�ƬP���м�ʱ�պϵ��S����ʱ����С��ֹ�Ҿ�Եϸ���������A�ļн�Ϊ�ȣ���Դ�綯��E������rһ��������˵������ȷ���ǣ�������
��ͼ��ʾ�ĵ�·��R1Ϊ�������裨����ֵ�����ܹ���ǿ�ȵ��������С�����þ�Եϸ�߰�һ����С����Ϊ���ɣ�ϵ��ƽ�а�������Ľ�����A���ڲ���森��R2�Ļ�ƬP���м�ʱ�պϵ��S����ʱ����С��ֹ�Ҿ�Եϸ���������A�ļн�Ϊ�ȣ���Դ�綯��E������rһ��������˵������ȷ���ǣ�������
 ��ͼ��ʾ�ĵ�·��R1Ϊ�������裨����ֵ�����ܹ���ǿ�ȵ��������С�����þ�Եϸ�߰�һ����С����Ϊ���ɣ�ϵ��ƽ�а�������Ľ�����A���ڲ���森��R2�Ļ�ƬP���м�ʱ�պϵ��S����ʱ����С��ֹ�Ҿ�Եϸ���������A�ļн�Ϊ�ȣ���Դ�綯��E������rһ��������˵������ȷ���ǣ�������
��ͼ��ʾ�ĵ�·��R1Ϊ�������裨����ֵ�����ܹ���ǿ�ȵ��������С�����þ�Եϸ�߰�һ����С����Ϊ���ɣ�ϵ��ƽ�а�������Ľ�����A���ڲ���森��R2�Ļ�ƬP���м�ʱ�պϵ��S����ʱ����С��ֹ�Ҿ�Եϸ���������A�ļн�Ϊ�ȣ���Դ�綯��E������rһ��������˵������ȷ���ǣ�������| A�� | ����R2�Ļ�����ͷP��a���ƶ�����ȱ�С | |
| B�� | ����R2�Ļ�����ͷP��b���ƶ�����ȱ�� | |
| C�� | ���ֻ�����ͷP�������ý�ǿ�Ĺ�����R1����С�����´ﵽ�ȶ���ȱ�С | |
| D�� | ���ֻ�����ͷP�������ý�ǿ�Ĺ�����R1����С�����´ﵽ�ȶ���Ȳ��� |
14�������Ϊ����б���ϣ�һľ�����ϻ�������t��ʱ�们��L�����ֹͣ����ľ����б���Ķ�Ħ��������ľ�����»���б������õ�ʱ��ֱ�Ϊ��������
| A�� | $\frac{2L}{g{t}^{2}cos��}$-tan����t$\sqrt{\frac{L}{g{t}^{2}sin��-L}}$ | B�� | $\frac{Lcos��}{g{t}^{2}}$-tan����t$\sqrt{\frac{gL}{{t}^{2}sin��-L}}$ | ||
| C�� | $\frac{Lsin��}{{t}^{2}}$-cos����t$\sqrt{\frac{gL}{{t}^{2}cos��-L}}$ | D�� | $\frac{Ltan��}{g{t}^{2}}$-cos����t$\sqrt{\frac{2gL}{g{t}^{2}-L}}$ |
11������ѡ�����й��ڵ�Ų���˵����ȷ���ǣ�������
| A�� | ����һ�ֵ�Ų� | |
| B�� | ��Ų��������˹Τͨ��ʵ�鷢�ֵ� | |
| C�� | ��Ų����Դ������� | |
| D�� | ��Ų��Ĵ���һ����Ҫ���� |
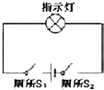
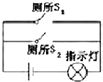
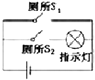
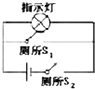
 Ҫ����ij��ѹ��V1������RV��������Ϊ2V������Լ2k����ʵ�����ṩ�������У�
Ҫ����ij��ѹ��V1������RV��������Ϊ2V������Լ2k����ʵ�����ṩ�������У�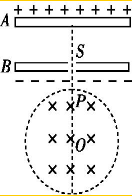 ��ͼ��ʾ��һ�Դ���ƽ�н�����A��Bˮƽ���ã������������ĵ��Ʋ�U=104V��������d=10-2m��B�����뿪��С��S�����������·���һ�뾶R=10-2m��Բ�ε���ǿ�ų����ų�����ֱ��ֽ������Ÿ�Ӧǿ�ȵĴ�СB=1T���ų������Բ��Oλ��С�����·���SO���߽�Բ�ı߽���P�㣮�Ⱥ�$\frac{q}{m}$=5��107C/kg�Ĵ������������ٶ�v=5��105m/s�Ӵų���ij��������Բ������ų��������ų���ƫת���ã�ǡ������OP�����С��S����糡������������SP���˶���ʱ����Բ��ƣ��������ӵ��������ƣ���
��ͼ��ʾ��һ�Դ���ƽ�н�����A��Bˮƽ���ã������������ĵ��Ʋ�U=104V��������d=10-2m��B�����뿪��С��S�����������·���һ�뾶R=10-2m��Բ�ε���ǿ�ų����ų�����ֱ��ֽ������Ÿ�Ӧǿ�ȵĴ�СB=1T���ų������Բ��Oλ��С�����·���SO���߽�Բ�ı߽���P�㣮�Ⱥ�$\frac{q}{m}$=5��107C/kg�Ĵ������������ٶ�v=5��105m/s�Ӵų���ij��������Բ������ų��������ų���ƫת���ã�ǡ������OP�����С��S����糡������������SP���˶���ʱ����Բ��ƣ��������ӵ��������ƣ���