题目内容
14.1957年第一颗人造卫星送上天,开辟了人类宇航的新时代.近五十年来,人类不仅发射了人造地球卫星,还向宇宙空间发射了多个空间探测器.空间探测器要飞向火星等其他行星,甚至飞出太阳系,首先要克服地球对它的引力的作用.理论研究表明,物体在地球附近都受到地球对它的万有引力的作用,具有引力势能,设物体在距地球无限远处的引力势能为零,则引力势能可以表示为E=-G$\frac{Mm}{r}$,其中G是万有引力常量,M是地球的质量,m是物体的质量,r是物体距地心的距离.已知:现有一个空间探测器随空间站一起绕地球做圆周运动,运行周期为T,已知探测器的质量为m,地球半径为R,地面附近的重力加速度为g.求:(1)该空间探测器环绕地球运动的线速度;
(2)要使这个空间探测器从空间站出发,脱离地球的引力作用,至少要对它做多少功.
分析 空间探测器随空间站一起绕地球做圆周运动,由地球的万有引力充当向心力,根据牛顿第二定律列式可求出空间站的轨道半径和速度,即可得到空间探测器具有的机械能.空间站要脱离地球的引力,机械能最小值为E∞=0,根据功能关系求功.
解答 解:(1)空间探测器绕地球作圆周运动,由$G\frac{Mm}{{r}^{2}}=m\frac{4{π}^{2}}{{T}^{2}}r$得空间站的轨道半径为:r=$\root{3}{\frac{{GMT}^{2}}{4{π}^{2}}}$
随空间站一起运动时,空间探测器的速度为:v=$\frac{2πr}{T}$=$\frac{2π}{T}\root{3}{\frac{{GMT}^{2}}{4{π}^{2}}}$=$\root{3}{\frac{2πGM}{T}}$
(2)空间探测器的动能为:$\frac{1}{2}{mv}^{2}$=$\frac{m}{2}\root{3}{(\frac{2πGM}{T})^{2}}$.
随空间站一起运动时,空间探测器具有的机械能为:
E1=-$G\frac{Mm}{r}$+$\frac{1}{2}{mv}^{2}$=$-\frac{GMm}{\root{3}{\frac{{GMT}^{2}}{4{π}^{2}}}}$+$\frac{m}{2}\root{3}{(\frac{2πGM}{T})^{2}}$=-$\frac{m}{2}\root{3}{{(\frac{2πGM}{T})}^{2}}$
空间站要脱离地球的引力,机械能最小值为E∞=0,因此,对探测器做功为:
W=E∞-E1=$\frac{m}{2}\root{3}{{(\frac{2πGM}{T})}^{2}}$
由地面附近的重力加速度g=G$\frac{M}{{R}^{2}}$ 得:W=$\frac{m}{2}\root{3}{{(\frac{2π{gR}^{2}}{T})}^{2}}$
答:(1)该空间探测器环绕地球运动的线速度为$\root{3}{\frac{2πGM}{T}}$.
(2)要使这个空间探测器从空间站出发,脱离地球的引力作用,至少要对它作$\frac{m}{2}\root{3}{{(\frac{2π{gR}^{2}}{T})}^{2}}$的功.
点评 对于卫星类型,要根据其运动模型,由万有引力定律、圆周运动规律和功能关系求解.

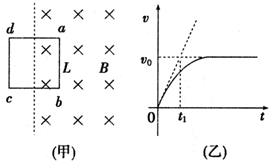 一有界匀强磁场区域如图(甲)所示,abcd是一个质量为m、电阻为R、边长为L、匝数为N的正方形线圈.线圈一半在磁场内,一半在磁场外.t=0时刻磁场磁感应强度由B0开始均匀减小,线圈在磁场力作用下运动,v-t图象如图(乙),图中斜向虚线为速度图线在0点的切线,数据由图中给出,不考虑重力影响.则磁场磁感应强度的变化率为( )
一有界匀强磁场区域如图(甲)所示,abcd是一个质量为m、电阻为R、边长为L、匝数为N的正方形线圈.线圈一半在磁场内,一半在磁场外.t=0时刻磁场磁感应强度由B0开始均匀减小,线圈在磁场力作用下运动,v-t图象如图(乙),图中斜向虚线为速度图线在0点的切线,数据由图中给出,不考虑重力影响.则磁场磁感应强度的变化率为( )| A. | $\frac{mR{v}_{0}}{{t}_{1}N{B}_{0}{L}^{3}}$ | B. | $\frac{2mR{v}_{0}}{{t}_{1}N{B}_{0}{L}^{2}}$ | ||
| C. | $\frac{mR{v}_{0}}{{t}_{1}{N}^{2}{B}_{0}{L}^{2}}$ | D. | $\frac{2mR{v}_{0}}{{t}_{1}{N}^{2}{B}_{0}{L}^{3}}$ |
| A. | 质点不受力运动轨迹可以是圆形 | |
| B. | 质点在变力作用下运动轨迹一定是曲线 | |
| C. | 质点受恒力作用运动轨迹可以是直线也可以是曲线 | |
| D. | 质点所受力的方向只要不变,轨迹就一定是直线 |
 如图所示,A,B是一对对置的平行金属板,中心分别有小孔P、Q,PQ连线垂直金属板,两板间距d=0.04m,从小孔P点处连续不断有质量为m=2×10-5的带正电的粒子沿着PQ方向放出.粒子的初速度和重力不计,从t0=0开始在AB间,加上沿PQ方向的匀强电场,场强E=2×103V/M,经过△t=0.02s 保持电场大小不变,而方向大小改变180°,试求:
如图所示,A,B是一对对置的平行金属板,中心分别有小孔P、Q,PQ连线垂直金属板,两板间距d=0.04m,从小孔P点处连续不断有质量为m=2×10-5的带正电的粒子沿着PQ方向放出.粒子的初速度和重力不计,从t0=0开始在AB间,加上沿PQ方向的匀强电场,场强E=2×103V/M,经过△t=0.02s 保持电场大小不变,而方向大小改变180°,试求: 从阴极K发射的电子经电势差U0=4500V的阳极加速后,沿平行于板面的方向从中央射入两块长L1=10cm,间距d=4cm的平行金属板AB之后,在离金属板边缘L2=75cm处放置一个直径D=20cm的带有记录纸的圆筒(如图所示),整个装置放在真空内,电子发射的初速度不计.已知电子质量m=0.9×10-30kg.
从阴极K发射的电子经电势差U0=4500V的阳极加速后,沿平行于板面的方向从中央射入两块长L1=10cm,间距d=4cm的平行金属板AB之后,在离金属板边缘L2=75cm处放置一个直径D=20cm的带有记录纸的圆筒(如图所示),整个装置放在真空内,电子发射的初速度不计.已知电子质量m=0.9×10-30kg.
 如图所示,在xoy坐标系坐标原点O处有一点状的放射源,它向xoy平面内的x轴上方各个方向发射α粒子,α粒子的速度大小均为v0,在0<y<d的区域内分布有指向y轴正方向的匀强电场,场强大小为E=$\frac{3mv_0^2}{2qd}$,其中q与m分别为α粒子的电量和质量;在d<y<2d的区域内分布有垂直于xoy平面向里的匀强磁场,mn为电场和磁场的边界.ab为一块很大的平面感光板垂直于xoy平面且平行于x轴,放置于y=2d处,如图所示.观察发现此时恰好无粒子打到ab板上.(q、d、m、v0均为已知量,不考虑α粒子的重力及粒子间的相互作用),求:
如图所示,在xoy坐标系坐标原点O处有一点状的放射源,它向xoy平面内的x轴上方各个方向发射α粒子,α粒子的速度大小均为v0,在0<y<d的区域内分布有指向y轴正方向的匀强电场,场强大小为E=$\frac{3mv_0^2}{2qd}$,其中q与m分别为α粒子的电量和质量;在d<y<2d的区域内分布有垂直于xoy平面向里的匀强磁场,mn为电场和磁场的边界.ab为一块很大的平面感光板垂直于xoy平面且平行于x轴,放置于y=2d处,如图所示.观察发现此时恰好无粒子打到ab板上.(q、d、m、v0均为已知量,不考虑α粒子的重力及粒子间的相互作用),求: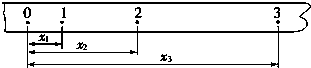 在做“练习使用打点计时器”的实验时,如图是某次实验的纸带,舍去前面比较密的点,从0点开始,每5个连续点取1个计数点,标以0、1、2、3…那么相邻两个计数点之间的时间间隔为T=0.1s,各计数点与0计数点之间的距离依次为x1=3.00cm、x2=7.50cm、x3=13.50cm,则打点计时器打记数点1时,物体的速度大小v1=0.375m/s,打点计时器打记数点2时,物体的速度大小V2=0.525m/s,物体运动的加速度=1.50m/s2.
在做“练习使用打点计时器”的实验时,如图是某次实验的纸带,舍去前面比较密的点,从0点开始,每5个连续点取1个计数点,标以0、1、2、3…那么相邻两个计数点之间的时间间隔为T=0.1s,各计数点与0计数点之间的距离依次为x1=3.00cm、x2=7.50cm、x3=13.50cm,则打点计时器打记数点1时,物体的速度大小v1=0.375m/s,打点计时器打记数点2时,物体的速度大小V2=0.525m/s,物体运动的加速度=1.50m/s2.