题目内容
9.假设地球同步卫星和月球都绕地球做匀速圆周运动,已知万有引力常量为G,地球质量为M,半径为R.地球的自转周期为T.月球到地心的距离为r,求:(1)月球的运行速度;
(2)同步卫星距离地面的高度;
(3)同步卫星和月球的运行周期之比.
分析 (1)月球绕地球的万有引力提供向心力,求出运行速度
(2)地球的同步卫星的万有引力提供向心力,可以求出地球同步卫星的高度.
(3)根据万有引力提供向心力求出月球的运行周期,再求比值
解答 解:(1)月球绕地球做匀速圆周运动,万有引力提供向心力,有:
$G\frac{Mm}{{r}_{\;}^{2}}=m\frac{{v}_{\;}^{2}}{r}$
解得:$v=\sqrt{\frac{GM}{r}}$
(2)同步卫星的万有引力提供向心力,周期等于地球的自转周期,有:
$G\frac{Mm′}{(R+h)_{\;}^{2}}=m′\frac{4{π}_{\;}^{2}}{{T}_{\;}^{2}}(R+h)$
解得:$h=\root{3}{\frac{GM{T}_{\;}^{2}}{4{π}_{\;}^{2}}}-R$
(3)月球绕地球运行做匀速圆周运动,有:$G\frac{Mm}{{r}_{\;}^{2}}=m\frac{4{π}_{\;}^{2}}{{T}_{\;}^{′2}}r$
解得:$T′=\sqrt{\frac{4{π}_{\;}^{2}{r}_{\;}^{3}}{GM}}$
同步卫星和月球的运行周期之比为:$\frac{T}{T′}=\frac{T}{\sqrt{\frac{4{π}_{\;}^{2}{r}_{\;}^{3}}{GM}}}=T\sqrt{\frac{GM}{4{π}_{\;}^{2}{r}_{\;}^{3}}}$
答:(1)月球的运行速度$\sqrt{\frac{GM}{r}}$;
(2)同步卫星距离地面的高度$\root{3}{\frac{GM{T}_{\;}^{2}}{4{π}_{\;}^{2}}}-R$;
(3)同步卫星和月球的运行周期之比$T\sqrt{\frac{GM}{4{π}_{\;}^{2}{r}_{\;}^{3}}}$.
点评 解答此题要清楚月球绕地球做匀速圆周运动靠万有引力提供向心力,地球的同步卫星的万有引力提供向心力且周期等于地球自转周期.

| A. | 沿电场线方向场强逐渐减小 | |
| B. | 同一电荷在电场线密的地方受电场力大 | |
| C. | 等势面上各点电场强度不可能相同 | |
| D. | 电场中电势高处,电荷的电势能大 |

| A. | 0.3 s和0.9s两时刻质点位移相同 | |
| B. | 0~0.3 s振子的加速度为正方向且增大 | |
| C. | 3 s时间内振子通过的路程一定为50 cm | |
| D. | 0.3~0.6 s和0.9~1.2 s两段时间内的速度方向相同 |
| A. | 示踪原子是利用放射性同位素的贯穿能力很强的性质 | |
| B. | 示踪原子是利用放射性同位素放出射线可被仪器探测的特点 | |
| C. | 射线探伤利用了射线贯穿能力很强的性质 | |
| D. | 射线探伤利用了射线电离能力很强的性质 |
 某同学利用DIS实验系统研究一定质量理想气体的状态变化,实验后计算机屏幕上显示出如图所示的pt图象.已知在状态B时气体的体积为VB=3L,则下列说法正确的是( )
某同学利用DIS实验系统研究一定质量理想气体的状态变化,实验后计算机屏幕上显示出如图所示的pt图象.已知在状态B时气体的体积为VB=3L,则下列说法正确的是( )| A. | 状态A到状态B气体的体积越来越大 | B. | 状态A的压强是0.5 atm | ||
| C. | 状态C体积是2 L | D. | 状态B到状态C气体的内能增加 |
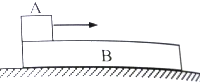 质量为m的滑块A的速度v沿水平方向滑到静止于水平光滑平面上足够长的物体B上,B的质量为M,AB间动摩擦因数为μ,问A在B上滑行多远时A相对B静止.
质量为m的滑块A的速度v沿水平方向滑到静止于水平光滑平面上足够长的物体B上,B的质量为M,AB间动摩擦因数为μ,问A在B上滑行多远时A相对B静止.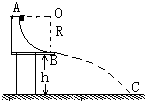 如图所示,在竖直平面内有$\frac{1}{4}$圆弧形轨道AB,其半径为1m,B点的切线恰好为水平方向.一个质量为2kg的小物体,从轨道顶端A由静止开始沿轨道滑下,到达轨道末端B点时的速度为4m/s,然后做平抛运动,落到地面上的C点,若轨道B端距地面高为h=5m,不计空气阻力,取g=10m/s2,求:
如图所示,在竖直平面内有$\frac{1}{4}$圆弧形轨道AB,其半径为1m,B点的切线恰好为水平方向.一个质量为2kg的小物体,从轨道顶端A由静止开始沿轨道滑下,到达轨道末端B点时的速度为4m/s,然后做平抛运动,落到地面上的C点,若轨道B端距地面高为h=5m,不计空气阻力,取g=10m/s2,求: