题目内容
18. 如图,用于水平方向成θ的力F,拉静止的质量为m的物体水平前进x后撤去拉力,已知物体和地面的动摩擦因素为μ,求:
如图,用于水平方向成θ的力F,拉静止的质量为m的物体水平前进x后撤去拉力,已知物体和地面的动摩擦因素为μ,求:(1)物体的最大速度;
(2)物体的最大位移x.
分析 根据牛顿第二定律求出在F作用下的加速度,根据速度位移公式求出物体的最大速度.根据牛顿第二定律求出撤去拉力后的加速度,结合速度位移公式求出匀减速运动的位移,从而得出物体的最大位移.
解答 解:(1)根据牛顿第二定律得,在F作用下的加速度$a=\frac{Fcosθ-μ(mg-Fsinθ)}{m}$,
根据v2=2ax得,物体的最大速度v=$\sqrt{2ax}$=$\sqrt{\frac{2[Fcosθ-μ(mg-Fsinθ)]x}{m}}$.
(2)撤去外力F后的加速度大小a′=μg,
则匀减速运动的位移大小$x′=\frac{{v}^{2}}{2a′}=\frac{a}{a′}x$=$\frac{[Fcosθ-μ(mg-Fsinθ)]}{μmg}$x.
物体的最大位移X=x+x′=x+$\frac{[Fcosθ-μ(mg-Fsinθ)]}{μmg}$x.
答:(1)物体的最大速度为$\sqrt{\frac{2[Fcosθ-μ(mg-Fsinθ)]x}{m}}$.
(2)物体的最大位移为x+$\frac{[Fcosθ-μ(mg-Fsinθ)]}{μmg}$x.
点评 本题考查了牛顿第二定律和运动学公式的综合运用,知道加速度是联系力学和运动学的桥梁,注意撤去拉力前后的摩擦力大小不同.

练习册系列答案
相关题目
8.某同学设计了一种静电除尘装置,如图1所示,其中有一长为L、宽为b、高为d的矩形通道,其前、后面板为绝缘材料,上、下面板为金属材料.图2是装置的截面图,上、下两板与电压恒定为U的高压直流电源相连.带负电的尘埃被吸入矩形通道的水平速度为v0,当碰到下板后其所带电荷被中和,同时被收集.将被收集尘埃的数量与进入矩形通道尘埃的数量的比值,称为除尘率.不计尘埃的重力及尘埃之间的相互作用.要增大除尘率,则下列措施可行的是( )


| A. | 只减小电压U | B. | 只增大宽度b | ||
| C. | 只增大尘埃被吸入水平速度v0 | D. | 只减小高度d |
9.下列说法正确的是( )
| A. | 质点是一种理想化模型 | |
| B. | 国际单位制中,力学的三个基本单位是千克、牛顿、秒 | |
| C. | 位移、力、质量都是矢量 | |
| D. | 亚里士多德提出力并不是维持物体运动的原因 |
13.一物体在竖直弹簧的上方h米处下落,然后又被弹簧弹回,则物体动能最大时是( )
| A. | 物体刚接触弹簧时 | B. | 物体重力与弹力相等时 | ||
| C. | 物体将弹簧压缩至最短时 | D. | 弹簧等于原长时 |
1.一个质子和一个中子聚变结合成一个氘核,同时辐射一个光子.已知质子、中子、氘核的质量分别为m1、m2、m3,普朗克常量为h,真空中的光速为c.下列说法正确的是( )
| A. | 核反应方程是${\;}_{1}^{1}H$+${\;}_{0}^{1}$n→${\;}_{1}^{3}$H+γ | |
| B. | 聚变反应中的质量亏损△m=m1+m2-m3 | |
| C. | 辐射出的光子的能量E=(m3-m1-m2)c2 | |
| D. | 光子的波长λ=$\frac{h}{({m}_{1}+{m}_{2}-{m}_{3}){c}^{2}}$ |

 如图,一个质量m=0.6kg的小球以初速度v0=3m/s从P点水平抛出,恰好从粗糙圆弧轨道ABC的A点沿切线方向进入轨道(不计空气阻力,进入圆弧轨道时无机械能损失).小球到达C点时的速度vC=4m/s,之后冲出圆弧轨道,向上到达最高点D后又落回C点,已知圆弧的半径R=0.5m,θ=53°,求:(g取10m/s2)
如图,一个质量m=0.6kg的小球以初速度v0=3m/s从P点水平抛出,恰好从粗糙圆弧轨道ABC的A点沿切线方向进入轨道(不计空气阻力,进入圆弧轨道时无机械能损失).小球到达C点时的速度vC=4m/s,之后冲出圆弧轨道,向上到达最高点D后又落回C点,已知圆弧的半径R=0.5m,θ=53°,求:(g取10m/s2)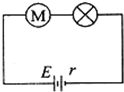 如图所示,电源电动势为E=30V,内阻为r=1Ω,电灯上标有“6V,12W”字样,直流电动机线圈电阻R=2Ω.若电灯恰能正常发光,则电动机输出的机械功率为36瓦.
如图所示,电源电动势为E=30V,内阻为r=1Ω,电灯上标有“6V,12W”字样,直流电动机线圈电阻R=2Ω.若电灯恰能正常发光,则电动机输出的机械功率为36瓦. 如图所示,一个质子以初速度v0=5×106m/s射入一个由两块带电的平行金属板组成的区域.两板距离为20cm,金属板之间是匀强电场,电场强度为3×105V/m.质子质量为m=1.67×10-27kg,电荷量为q=1.60×10-19C.试求
如图所示,一个质子以初速度v0=5×106m/s射入一个由两块带电的平行金属板组成的区域.两板距离为20cm,金属板之间是匀强电场,电场强度为3×105V/m.质子质量为m=1.67×10-27kg,电荷量为q=1.60×10-19C.试求