题目内容
15. 如图所示,两个可视为质点的、相同的木块甲和乙放在转盘上,两者用长为L的细绳连接(细绳能够承受足够大的拉力),木块与转盘的最大静摩擦力均为各自重力的K倍,两物体间连一细线,此线过圆心.甲到圆心距离r1,乙到圆心距离r2,且r1=$\frac{L}{4},{r_2}=\frac{3L}{4}$,水平圆盘可绕过圆心的竖直轴00’转动,两物体随圆盘一起以角速度ω做匀速转动.下述所取ω值范围已保证甲和乙相对圆盘无滑动,则:(已知重力加速度为g)( )
如图所示,两个可视为质点的、相同的木块甲和乙放在转盘上,两者用长为L的细绳连接(细绳能够承受足够大的拉力),木块与转盘的最大静摩擦力均为各自重力的K倍,两物体间连一细线,此线过圆心.甲到圆心距离r1,乙到圆心距离r2,且r1=$\frac{L}{4},{r_2}=\frac{3L}{4}$,水平圆盘可绕过圆心的竖直轴00’转动,两物体随圆盘一起以角速度ω做匀速转动.下述所取ω值范围已保证甲和乙相对圆盘无滑动,则:(已知重力加速度为g)( )| A. | 若ω≤2$\sqrt{\frac{Kg}{3L}}$时,甲、乙所受静摩擦力都指向圆心 | |
| B. | ω取不同值时,甲所受静摩擦力始终指向圆心;乙所受静摩擦力可能指向圆心,也可能背向圆心 | |
| C. | ω取不同值时,乙所受静摩擦力始终指向圆心;甲所受静摩擦力可能指向圆心,也可能背向圆心 | |
| D. | 如果ω>2$\sqrt{\frac{Kg}{L}}$时,两物体将相对圆盘发生滑动 |
分析 甲乙两物体随盘一起做匀速转动,保持相对静止,角速度相等,随着角速度的增大,乙先达到最大静摩擦力,角速度继续增大,绳子的拉力逐渐增大,甲所受的静摩擦力逐渐减小,当P的静摩擦力减小到零,又反向增大,增大到最大值时,角速度再增大,甲乙与圆盘之间发生相对滑动.
解答 解:甲乙随转盘一起做匀速圆周运动,由于乙的半径较大,故需要的向心力较大,故Kmg=mω2r2,解得ω=2$\sqrt{\frac{Kg}{3L}}$,即若ω≤2$\sqrt{\frac{Kg}{3L}}$时,甲、乙所受静摩擦力都指向圆心,故A正确;
B、根据Kmg=mrω2得,$ω=\sqrt{\frac{Kg}{r}}$,乙的半径大,知乙先达到最大静摩擦力.当角速度增大,绳子出现张力,乙靠张力和静摩擦力的合力提供向心力,甲也靠拉力和静摩擦力的合力提供向心力,角速度增大,绳子的拉力逐渐增大,甲所受的静摩擦力先减小后反向增大,当反向增大到最大值,角速度再增大,甲乙与圆盘发生相对滑动.所以乙所受的静摩擦力方向始终指向圆心,甲所受的静摩擦力方向先指向圆心,然后背离圆心,故B错误,C正确;
D、设角速度为ω时,此时甲乙发生滑动,此时绳子的拉力为F,则F-Kmg=mω2r1,F+Kmg=mω2r2,解得ω=2$\sqrt{\frac{Kg}{L}}$,故ω>2$\sqrt{\frac{Kg}{L}}$时,两物体将相对圆盘发生滑动,故D正确;
故选:ACD
点评 本题是匀速圆周运动中连接体问题,既要隔离研究,也要抓住它们之间的联系:角速度相等、绳子拉力大小相等.

练习册系列答案
相关题目
5.下列说法正确的是( )
| A. | 光纤通信及医用纤维式内窥镜都是利用了光的全反射原理 | |
| B. | 肥皂泡呈现的彩色是光的干涉现象,露珠呈现的彩色的是光的色散现象 | |
| C. | 电磁波中电场能量最大时,磁场能量为零;磁场能量最大时,电场能量为零 | |
| D. | 照相机镜头上会镀一层膜,有时会在镜头前加一个偏振片,这样做都是为了增加光的透射强度 | |
| E. | 火箭以接近光速飞跃地球,火箭上的人看到的火箭的长度比地球上的人看到的火箭的长度长 |
6. 如图所示,有两个穿着溜冰鞋的人站在水平冰面上,当其中某人A从背后轻轻推另一个人B时,两个人会向相反的方向运动,不计摩擦力,则下列判断正确的是( )
如图所示,有两个穿着溜冰鞋的人站在水平冰面上,当其中某人A从背后轻轻推另一个人B时,两个人会向相反的方向运动,不计摩擦力,则下列判断正确的是( )
 如图所示,有两个穿着溜冰鞋的人站在水平冰面上,当其中某人A从背后轻轻推另一个人B时,两个人会向相反的方向运动,不计摩擦力,则下列判断正确的是( )
如图所示,有两个穿着溜冰鞋的人站在水平冰面上,当其中某人A从背后轻轻推另一个人B时,两个人会向相反的方向运动,不计摩擦力,则下列判断正确的是( )| A. | A、B的质量一定相等 | B. | 推后两人的动能一定相等 | ||
| C. | 推后两人的总动量一定为0 | D. | 推后两人的速度大小一定相等 |
3.质量为1kg的小球A以2m/s的速度与质量为2kg的静止小球B发生正碰,关于碰后的速度vA和vB,可能正确的是( )
| A. | vA=3 m/s,vB=-0.5 m/s | B. | vA=vB=$\frac{2}{3}$m/s | ||
| C. | vA=1 m/s,vB=1.5 m/s | D. | vA=-0.5 m/s,vB=1.25m/s |
10.质量为m的物体做自由落体运动,经过时间t落地.在物体下落的过程中,以下说法正确的是( )
| A. | 下落过程中,重力的平均功率为$\frac{1}{2}$mg2t | |
| B. | 下落过程中,重力的平均功率为mg2t | |
| C. | 落地前瞬间,重力的瞬时功率为$\frac{1}{2}$mg2t | |
| D. | 落地前瞬间,重力的瞬时功率为mg2t |
20. 如图为氢原子的能级示意图,锌的逸出功是3.34eV,那么对氢原子在能级跃迁过程中发射或吸收光子的规律认识错误的是( )
如图为氢原子的能级示意图,锌的逸出功是3.34eV,那么对氢原子在能级跃迁过程中发射或吸收光子的规律认识错误的是( )
 如图为氢原子的能级示意图,锌的逸出功是3.34eV,那么对氢原子在能级跃迁过程中发射或吸收光子的规律认识错误的是( )
如图为氢原子的能级示意图,锌的逸出功是3.34eV,那么对氢原子在能级跃迁过程中发射或吸收光子的规律认识错误的是( )| A. | 用能量为14.0eV的光子照射,可使处于基态的氢原子电离 | |
| B. | 一群处于n=4能级的氢原子向低能级跃迁所辐射的光中,有3种不同频率的光能使锌发生光电效应 | |
| C. | 一群处于n=3能级的氢原子向基态跃迁时,发出的光照射锌板,锌板表面所发出的光电子的最大初动能为8.75eV | |
| D. | 用能量为10.21eV 的光子照射,可使处于基态的氢原子跃迁到激发态 |
7. 一圆盘可绕通过其中心且垂直于盘面的竖直轴转动,现在圆盘上放置一个木块,当圆盘匀速转动时,木块随圆盘一起运动(保持相对静止),如图所示,那么下列说法正确的是( )
一圆盘可绕通过其中心且垂直于盘面的竖直轴转动,现在圆盘上放置一个木块,当圆盘匀速转动时,木块随圆盘一起运动(保持相对静止),如图所示,那么下列说法正确的是( )
 一圆盘可绕通过其中心且垂直于盘面的竖直轴转动,现在圆盘上放置一个木块,当圆盘匀速转动时,木块随圆盘一起运动(保持相对静止),如图所示,那么下列说法正确的是( )
一圆盘可绕通过其中心且垂直于盘面的竖直轴转动,现在圆盘上放置一个木块,当圆盘匀速转动时,木块随圆盘一起运动(保持相对静止),如图所示,那么下列说法正确的是( )| A. | 木块受到重力、支持力、摩擦力、向心力的作用 | |
| B. | 木块受到重力、支持力、摩擦力的作用 | |
| C. | 木块受到的摩擦力,方向与木块的运动速度方向相反 | |
| D. | 逐渐增大圆盘转速,木块不会发生滑动 |
6.如图是物体做直线运动的v-t图象,由图可知,该物体( )


| A. | 第1s内和第3s内的运动方向相反 | B. | 第3s内和第4s内的加速度不相同 | ||
| C. | 第1s内和第4s内的位移大小相等 | D. | 0~2s和0~4s内的平均速度大小相等 |
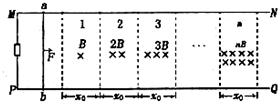 如图所示.两平行光滑的金属导轨MN、PQ固定在水平面上,相距为L,处于竖直向下的磁场中,整个磁场由n个宽度皆为x0的条形匀强磁场区域1、2…n组成,从左向右依次排列,磁感应强度的大小分别为B、2B、3B…nB,两导轨左端MP间接入电阻R,一质量为m的金属棒ab垂直于MN、PQ放在水平导轨上,与导轨电接触良好,不计导轨和金属棒的电阻.
如图所示.两平行光滑的金属导轨MN、PQ固定在水平面上,相距为L,处于竖直向下的磁场中,整个磁场由n个宽度皆为x0的条形匀强磁场区域1、2…n组成,从左向右依次排列,磁感应强度的大小分别为B、2B、3B…nB,两导轨左端MP间接入电阻R,一质量为m的金属棒ab垂直于MN、PQ放在水平导轨上,与导轨电接触良好,不计导轨和金属棒的电阻.