题目内容
2．
飞机做俯冲拉起运动时，在最低点附近做半径为r=200m的圆周运动（如图）．如果飞行员的质量m=70kg，飞机经过最低点P时的速度v=360km/h，求这时飞行员对座位的压力．
分析 在最低点，飞行员靠重力和支持力的合力提供向心力，根据牛顿第二定律气促支持力的大小，从而得出飞行员对座位的压力大小．
解答 解：360km/h=100m/s
在最低点，根据牛顿第二定律得，N-mg=m$\frac{{v}^{2}}{r}$，
解得N=$mg+m\frac{{v}^{2}}{r}=700+70×\frac{10{0}^{2}}{200}N$=4200N．
则飞行员对座位的压力为4200N．
答：飞行员对座位的压力为4200N．
点评 解决本题的关键知道圆周运动向心力的来源，结合牛顿第二定律进行求解，基础题．
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
12．
如图所示，AC、BD为圆的两条互相垂直的直径，圆心为O，将带有等量电荷q的正、负点电荷放在圆周上，它们的位置关于AC对称．要使圆心O处的电场强度为零，可在圆周上再放置一个带适当电荷量的正点电荷+Q，则该点电荷+Q应放在（ ）
如图所示，AC、BD为圆的两条互相垂直的直径，圆心为O，将带有等量电荷q的正、负点电荷放在圆周上，它们的位置关于AC对称．要使圆心O处的电场强度为零，可在圆周上再放置一个带适当电荷量的正点电荷+Q，则该点电荷+Q应放在（ ）| A． | A点 | B． | B点 | C． | C点 | D． | D点 |
如图所示，火箭平台上放有测试仪器，火箭从地面起动后，以加速度$\frac{g}{2}$竖直向上匀加速运动，升到某一高度时，测试仪器对平台的压力为起动前压力的$\frac{17}{18}$，已知地球半径为R，求火箭此时离地面的高度（g为地面附近的重力加速度）
17．
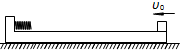如图所示，一块质量为M的木板停在光滑的水平面上，木板的左端有挡板，挡板上固定一个小弹簧．一个质量为m的小物块（可视为质点）以水平速度υ0从木板的右端开始向左运动，与弹簧碰撞后（弹簧处于弹性限度内），最终又恰好停在木板的右端．根据上述情景和已知量，可以求出（ ）
如图所示，一块质量为M的木板停在光滑的水平面上，木板的左端有挡板，挡板上固定一个小弹簧．一个质量为m的小物块（可视为质点）以水平速度υ0从木板的右端开始向左运动，与弹簧碰撞后（弹簧处于弹性限度内），最终又恰好停在木板的右端．根据上述情景和已知量，可以求出（ ）| A． | 弹簧的劲度系数 | |
| B． | 弹簧的最大弹性势能 | |
| C． | 木板和小物块组成的系统最终损失的机械能 | |
| D． | 若再已知木板长度l可以求出木板和小物块间的动摩擦因数 |
7．
如图所示，A、B两物体的质量比mA：mB=3：8，它们原来静止在平板车C上，A、B间有一根被压缩了的弹簧，A、B与平板车上表面间动摩擦因数相同，地面水平光滑，突然释放弹簧后，则有（ ）
如图所示，A、B两物体的质量比mA：mB=3：8，它们原来静止在平板车C上，A、B间有一根被压缩了的弹簧，A、B与平板车上表面间动摩擦因数相同，地面水平光滑，突然释放弹簧后，则有（ ）| A． | A、B系统动量守恒 | B． | A、B、C系统动量守恒 | ||
| C． | 小车向左运动 | D． | 小车向右运动 |
11．设同步卫星离地心的距离为r，运行速率为v1，加速度为a1；地球赤道上的物体随地球自转的向心加速度为a2，第一宇宙速度为v2，地球的半径为R，则下列比值正确的是（ ）
| A． | $\frac{v_1}{v_2}=\sqrt{\frac{r}{R}}$ | B． | $\frac{a_1}{a_2}=\frac{r^2}{R^2}$ | C． | $\frac{a_1}{a_2}=\frac{R^2}{r^2}$ | D． | $\frac{v_1}{v_2}=\sqrt{\frac{R}{r}}$ |
12．关于圆周运动的速度和加速度的关系，下列论述正确的是（ ）
| A． | 速度的变化量越大，加速度也越大 | |
| B． | 速度方向变化越快，向心加速度越大 | |
| C． | 速度大小变化的快慢与向心加速度大小无关 | |
| D． | 速度方向的变化率越大，向心加速度越大 |