题目内容
1.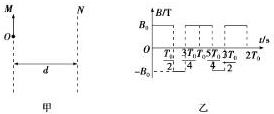 如图甲所示,M、N是宽为d的两竖直线,其间存在垂直纸面方向的磁场(未画出),磁感应强度随时间按图乙所示规律变化(垂直纸面向外为正,T0为已知),现有一个质量为m、电荷量为+q的离子在t=0时从直线M上的O点沿着OM线射入磁场,离子重力不计,离子恰好不能从右边界穿出且在2T0时恰好返回左边界M,则图乙中磁感应强度B0的大小和离子的初速度v0分别为( )
如图甲所示,M、N是宽为d的两竖直线,其间存在垂直纸面方向的磁场(未画出),磁感应强度随时间按图乙所示规律变化(垂直纸面向外为正,T0为已知),现有一个质量为m、电荷量为+q的离子在t=0时从直线M上的O点沿着OM线射入磁场,离子重力不计,离子恰好不能从右边界穿出且在2T0时恰好返回左边界M,则图乙中磁感应强度B0的大小和离子的初速度v0分别为( )| A. | B0=$\frac{2πm}{q{T}_{0}}$,v0=$\frac{πd}{{T}_{0}}$ | B. | B0=$\frac{2πm}{q{T}_{0}}$,v0=$\frac{πd}{{2T}_{0}}$ | ||
| C. | B0=$\frac{πm}{q{T}_{0}}$,v0=$\frac{πd}{{T}_{0}}$ | D. | B0=$\frac{πm}{q{T}_{0}}$,v0=$\frac{πd}{{2T}_{0}}$ |
分析 根据对称性,粒子在t=${T}_{0}^{\;}$时刻恰好到达右边界,因为恰好不从右边界穿出,速度方向和右边界平行,只有一种情景,即$0-\frac{{T}_{0}^{\;}}{2}$顺时针运动半圈,$\frac{{T}_{0}^{\;}}{2}-\frac{3{T}_{0}^{\;}}{4}$逆时针运动四分之一圆,$\frac{3{T}_{0}^{\;}}{4}-{T}_{0}^{\;}$顺时针运动四分之一圆正好和右边界相切,然后${T}_{0}^{\;}-\frac{5{T}_{0}^{\;}}{4}$顺时针四分之一圆,$\frac{5{T}_{0}^{\;}}{4}-\frac{3{T}_{0}^{\;}}{2}$逆时针四分之一圆,$\frac{3{T}_{0}^{\;}}{2}-2{T}_{0}^{\;}$顺时针运动半圈返回左边界M.利用几何知识求出半径,利用圆周运动的规律求出待求量.
解答  解:根据题意,根据带电子在磁场中运动的过程的分析,洛伦兹力不做功,根据$q{v}_{0}^{\;}B=m\frac{{v}_{0}^{2}}{r}$得$r=\frac{m{v}_{0}^{\;}}{qB}$,磁场虽然方向改变但大小不变,所以半径不变,由以上分析知,MN之间距离d=4r,由以上分析知带电粒子匀速圆周运动一个周期的时间T等于磁感应强度随时间变化的周期${T}_{0}^{\;}$,即$T={T}_{0}^{\;}$①
解:根据题意,根据带电子在磁场中运动的过程的分析,洛伦兹力不做功,根据$q{v}_{0}^{\;}B=m\frac{{v}_{0}^{2}}{r}$得$r=\frac{m{v}_{0}^{\;}}{qB}$,磁场虽然方向改变但大小不变,所以半径不变,由以上分析知,MN之间距离d=4r,由以上分析知带电粒子匀速圆周运动一个周期的时间T等于磁感应强度随时间变化的周期${T}_{0}^{\;}$,即$T={T}_{0}^{\;}$①
带电粒子圆周运动的周期公式$T=\frac{2πm}{q{B}_{0}^{\;}}$②
联立①②式得${T}_{0}^{\;}=\frac{2πm}{q{B}_{0}^{\;}}$,解得${B}_{0}^{\;}=\frac{2πm}{q{T}_{0}^{\;}}$③
MN之间的距离d=4r即$r=\frac{d}{4}$④
带电粒子圆周运动的半径公$r=\frac{m{v}_{0}^{\;}}{q{B}_{0}^{\;}}$⑤
联立③④⑤得${v}_{0}^{\;}=\frac{πd}{2{T}_{0}^{\;}}$
故选:B
点评 根据带电粒子在洛伦兹力作用下做匀速圆周运动,依据几何关系求出半径,分析清楚运动情景,得到磁场变化周期与带电粒子运动周期之间关系很重要.

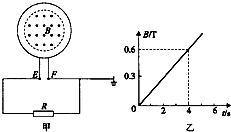 如图甲所示,一个圆形线圈匝数n=50匝、面积S1=0.5m2、电阻r=1Ω.有一个R=2Ω的电阻,将其两端E、F分别与图甲中的圆形线圈相连接,F端接地.在线圈中存在面积S2=0.4m2的垂直线圈平面向外的匀强磁场区域,磁感应强度B随时间t变化的关系如图乙所示,则下列说法正确的是( )
如图甲所示,一个圆形线圈匝数n=50匝、面积S1=0.5m2、电阻r=1Ω.有一个R=2Ω的电阻,将其两端E、F分别与图甲中的圆形线圈相连接,F端接地.在线圈中存在面积S2=0.4m2的垂直线圈平面向外的匀强磁场区域,磁感应强度B随时间t变化的关系如图乙所示,则下列说法正确的是( )| A. | 圆形线圈中产生的感应电动势E=3V | |
| B. | 在0~4s时间内通过电阻的电荷量g=6C | |
| C. | 设F端电势为零,则E端的电势φE=2V | |
| D. | 在0~4s时间内电阻R上产生的焦耳热Q=8J |
| A. | $\frac{KQ}{{R}^{2}}$ | B. | $\frac{2KQ}{{R}^{2}}$ | C. | $\frac{\sqrt{3}KQ}{{R}^{2}}$ | D. | $\frac{\sqrt{5}KQ}{{R}^{2}}$ |
| A. | 该卫星一定是地球同步卫星 | |
| B. | 该卫星轨道平 面与南纬31°52′所确定的平面共面 | |
| C. | 该卫星运行周期一定是地球自转周期的整数倍 | |
| D. | 地球自转周期一定是该卫星运行周期的整数倍 |
| A. | 做功和热传递是改变物体内能的两种本质不同的物理过程,做功是其他形式的能和内能之间的转化;热传递则是物体内能的转移 | |
| B. | 外界对物体做功,物体的内能一定增大 | |
| C. | 温度高的物体其热量必定多,内能必定大 | |
| D. | 热水的内能比冷水的内能多 |
 在如图所示的电路中,由于某一电阻发生短路或断路,A灯变暗,B灯变亮,则故障可能是( )
在如图所示的电路中,由于某一电阻发生短路或断路,A灯变暗,B灯变亮,则故障可能是( )| A. | R1短路 | B. | R2断路 | C. | R3短路 | D. | R4断路 |

| A. | 当地的重力加速度大小为$\frac{b}{R}$ | |
| B. | 小球的质量为$\frac{b}{a}$R | |
| C. | 若c=2b,则v2=c时杆对小球拉力的大小为a | |
| D. | 若c=2b,则v2=c时杆对小球支持力的大小为2a |
 制作“棉花”糖的原理:内筒与洗衣机的脱水筒相似,里面加入白砂糖,加热使糖熔化成糖汁.内筒高速旋转,黏稠的糖汁就做离心运动,由于惯性从内筒壁的小孔沿切线方向飞散出去,成为丝状到达温度较低的外筒,并迅速冷却凝固,变得纤细雪白,像一团团棉花.
制作“棉花”糖的原理:内筒与洗衣机的脱水筒相似,里面加入白砂糖,加热使糖熔化成糖汁.内筒高速旋转,黏稠的糖汁就做离心运动,由于惯性从内筒壁的小孔沿切线方向飞散出去,成为丝状到达温度较低的外筒,并迅速冷却凝固,变得纤细雪白,像一团团棉花. 如图甲所示,水平挡板A和竖直挡板B固定在斜面C上,一质量为m的光滑小球恰能与两挡板和斜面同时接触.挡板A、B和斜面C对小球的弹力大小分别为FA、FB和FC.现使斜面和物体一起在水平面上水平向左做加速度为a的匀加速直线运动.若FA和FB不会同时存在,斜面倾角为θ,重力加速度为g,则图乙所列图象中,可能正确的是( )
如图甲所示,水平挡板A和竖直挡板B固定在斜面C上,一质量为m的光滑小球恰能与两挡板和斜面同时接触.挡板A、B和斜面C对小球的弹力大小分别为FA、FB和FC.现使斜面和物体一起在水平面上水平向左做加速度为a的匀加速直线运动.若FA和FB不会同时存在,斜面倾角为θ,重力加速度为g,则图乙所列图象中,可能正确的是( )


