��Ŀ����
4��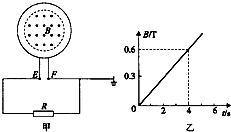 ��ͼ����ʾ��һ��Բ����Ȧ����n=50�ѡ����S1=0.5m2������r=1������һ��R=2���ĵ��裬��������E��F�ֱ���ͼ���е�Բ����Ȧ�����ӣ�F�˽ӵأ�����Ȧ�д������S2=0.4m2�Ĵ�ֱ��Ȧƽ���������ǿ�ų����Ÿ�Ӧǿ��B��ʱ��t�仯�Ĺ�ϵ��ͼ����ʾ��������˵����ȷ���ǣ�������
��ͼ����ʾ��һ��Բ����Ȧ����n=50�ѡ����S1=0.5m2������r=1������һ��R=2���ĵ��裬��������E��F�ֱ���ͼ���е�Բ����Ȧ�����ӣ�F�˽ӵأ�����Ȧ�д������S2=0.4m2�Ĵ�ֱ��Ȧƽ���������ǿ�ų����Ÿ�Ӧǿ��B��ʱ��t�仯�Ĺ�ϵ��ͼ����ʾ��������˵����ȷ���ǣ�������| A�� | Բ����Ȧ�в����ĸ�Ӧ�綯��E=3V | |
| B�� | ��0��4sʱ����ͨ������ĵ����g=6C | |
| C�� | ��F�˵���Ϊ�㣬��E�˵ĵ��Ʀ�E=2V | |
| D�� | ��0��4sʱ���ڵ���R�ϲ����Ľ�����Q=8J |
���� �ɷ����ڵ�Ÿ�Ӧ���ɿ��������Ӧ�綯�ƣ�
��ŷķ��������������ɵ�������ʽ����������
����ζ��ɿ����жϳ���Ӧ��������Ȼ���жϵ��Ƹߵͣ�
�ɽ������ɿ�����������ȣ�
��� �⣺A����Ȧ�����ĵ綯�ƣ�E=n$\frac{��∅}{��t}$=n$\frac{��B}{��t}$S=50��$\frac{0.6}{4}$��0.4=3V����A��ȷ��
B������Ϊ��I=$\frac{E}{R+r}$=$\frac{3}{2+1}$=1A��ͨ������R�ĵ����Ϊ��q=It=1��4=4C����B����
C������ζ��ɿ�֪��������˳ʱ�뷽��F����Ƹߣ�E����Ƶͣ�UR=IR=1��2=2V��UR=��F-��E����E=-2V����C����
D����0��4sʱ���ڵ���R�ϲ����Ľ�����Ϊ��Q=I2Rt=12��2��4=8J����D��ȷ��
��ѡ��AD��
���� ���⿼������綯�ơ�����������ơ������ȵȣ�Ӧ�÷����ڵ�Ÿ�Ӧ���ɡ�ŷķ���ɡ���������ʽ���������ɼ�����ȷ���⣮

��ϰ��ϵ�д�
 �¿α�����Ķ�ѵ��ϵ�д�
�¿α�����Ķ�ѵ��ϵ�д�
�����Ŀ
14��������һ��Բ���˶�ʱ��������������˵���в�ȷ���ǣ�������
���������Dz������ļ��ٶȵ���
���������������ܵ��ĺ�����
���������������Ǹı������ٶȵķ���
������������Բ���˶�ʱ���ܵ����������Ǻ�����
���������Dz������ļ��ٶȵ���
���������������ܵ��ĺ�����
���������������Ǹı������ٶȵķ���
������������Բ���˶�ʱ���ܵ����������Ǻ�����
| A�� | �� | B�� | �٢� | C�� | �� | D�� | �ڢ� |
12�������������˶�ʱ������˵����ȷ���ǣ�������
| A�� | �ٶȵķ��Ϸ����仯���ٶȵĴ�С��һ�������仯 | |
| B�� | �������˶����������һ���DZ��� | |
| C�� | ���������˶����ٶ�һ�������仯�����Լ��ٶ�һ��Ҳ���ϱ仯�� | |
| D�� | ����Բ���˶����ٶȴ�С���䣬�����������м��ٶ� |
9�����������У����������˶����ǣ�������
| A�� | ������ɲ��ʱ���˿���ǰ�� | |
| B�� | ����ת��ʱ�ٶȹ��˿о�����˦ | |
| C�� | ϴ�·���ˮͰ��ʼת�����·���Ͱ���ĵ�������Ͱ���� | |
| D�� | �˶�ԱͶ������ʱ���ڸ�����ת��ʱ���ͷ����� |
16������˵����ȷ���ǣ�������
| A�� | ��ͨ�������仯ʱ���Ÿ�Ӧǿ��Ҳһ�������仯 | |
| B�� | ������Ȧ�Ĵ�ͨ��Ϊ�㣬��Ӧ�綯��һ��Ϊ�� | |
| C�� | ������Ȧ�Ĵ�ͨ���仯Խ�죬��Ӧ�綯��Խ�� | |
| D�� | �����谭�ĺ��壬��Ӧ�����Ĵų��ܺͻ�·��ԭ�ų��ķ����෴ |
1��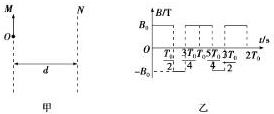 ��ͼ����ʾ��M��N�ǿ�Ϊd������ֱ�ߣ������ڴ�ֱֽ�淽��Ĵų���δ���������Ÿ�Ӧǿ����ʱ�䰴ͼ����ʾ���ɱ仯����ֱֽ������Ϊ����T0Ϊ��֪��������һ������Ϊm�������Ϊ+q��������t=0ʱ��ֱ��M�ϵ�O������OM������ų��������������ƣ�����ǡ�ò��ܴ��ұ߽紩������2T0ʱǡ�÷�����߽�M����ͼ���дŸ�Ӧǿ��B0�Ĵ�С�����ӵij��ٶ�v0�ֱ�Ϊ��������
��ͼ����ʾ��M��N�ǿ�Ϊd������ֱ�ߣ������ڴ�ֱֽ�淽��Ĵų���δ���������Ÿ�Ӧǿ����ʱ�䰴ͼ����ʾ���ɱ仯����ֱֽ������Ϊ����T0Ϊ��֪��������һ������Ϊm�������Ϊ+q��������t=0ʱ��ֱ��M�ϵ�O������OM������ų��������������ƣ�����ǡ�ò��ܴ��ұ߽紩������2T0ʱǡ�÷�����߽�M����ͼ���дŸ�Ӧǿ��B0�Ĵ�С�����ӵij��ٶ�v0�ֱ�Ϊ��������
 ��ͼ����ʾ��M��N�ǿ�Ϊd������ֱ�ߣ������ڴ�ֱֽ�淽��Ĵų���δ���������Ÿ�Ӧǿ����ʱ�䰴ͼ����ʾ���ɱ仯����ֱֽ������Ϊ����T0Ϊ��֪��������һ������Ϊm�������Ϊ+q��������t=0ʱ��ֱ��M�ϵ�O������OM������ų��������������ƣ�����ǡ�ò��ܴ��ұ߽紩������2T0ʱǡ�÷�����߽�M����ͼ���дŸ�Ӧǿ��B0�Ĵ�С�����ӵij��ٶ�v0�ֱ�Ϊ��������
��ͼ����ʾ��M��N�ǿ�Ϊd������ֱ�ߣ������ڴ�ֱֽ�淽��Ĵų���δ���������Ÿ�Ӧǿ����ʱ�䰴ͼ����ʾ���ɱ仯����ֱֽ������Ϊ����T0Ϊ��֪��������һ������Ϊm�������Ϊ+q��������t=0ʱ��ֱ��M�ϵ�O������OM������ų��������������ƣ�����ǡ�ò��ܴ��ұ߽紩������2T0ʱǡ�÷�����߽�M����ͼ���дŸ�Ӧǿ��B0�Ĵ�С�����ӵij��ٶ�v0�ֱ�Ϊ��������| A�� | B0=$\frac{2��m}{q{T}_{0}}$��v0=$\frac{��d}{{T}_{0}}$ | B�� | B0=$\frac{2��m}{q{T}_{0}}$��v0=$\frac{��d}{{2T}_{0}}$ | ||
| C�� | B0=$\frac{��m}{q{T}_{0}}$��v0=$\frac{��d}{{T}_{0}}$ | D�� | B0=$\frac{��m}{q{T}_{0}}$��v0=$\frac{��d}{{2T}_{0}}$ |

 ijͬѧ����ͼ����ʾװ�������о�ƽ���˶�����ʵ�飮����ʵ����������ֽ�������С��ˮƽ�׳�����˶��켣�������������й켣ͼ�ߵ�����ֽ��ʧ��һ���֣�ʣ�ಿ����ͼ����ʾ��ͼ��ˮƽ��������ֱ����ÿС��ij��Ⱦ�����0.10m��P1��P2��P3�ǹ켣ͼ���ϵ�3���㣬P1��P2��P2��P3֮���ˮƽ������ȣ����������գ����������ٶ�ȡ10m/s2��
ijͬѧ����ͼ����ʾװ�������о�ƽ���˶�����ʵ�飮����ʵ����������ֽ�������С��ˮƽ�׳�����˶��켣�������������й켣ͼ�ߵ�����ֽ��ʧ��һ���֣�ʣ�ಿ����ͼ����ʾ��ͼ��ˮƽ��������ֱ����ÿС��ij��Ⱦ�����0.10m��P1��P2��P3�ǹ켣ͼ���ϵ�3���㣬P1��P2��P2��P3֮���ˮƽ������ȣ����������գ����������ٶ�ȡ10m/s2��