题目内容
20.已知人造航天器在月球表面上空绕月球做匀速圆周运动,经时间t(t小于航天器的绕行周期),航天器运动的弧长为s,航天器与月球的中心连线扫过角度为θ,引力常量为G,则( )| A. | 航天器的轨道半径为$\frac{θ}{s}$ | B. | 航天器的环绕周期为$\frac{2πt}{θ}$ | ||
| C. | 月球的质量为$\frac{s^2}{{G{t^2}θ}}$ | D. | 月球的密度为$\frac{3{θ}^{2}}{4G{t}^{2}}$ |
分析 由万有引力充当向心力而做圆周运动的,则由万有引力公式及已知量可得出能计算的物理量.
解答 解:A、根据几何关系得:r=$\frac{s}{θ}$.故A错误;
B、经过时间t,航天器与月球的中心连线扫过角度为θ则:$\frac{t}{T}=\frac{θ}{2}$,得:T=$\frac{2πt}{θ}$.故B正确;
C、由万有引力充当向心力而做圆周运动,所以:$\frac{GMm}{r^2}=mr\frac{{4{π^2}}}{T^2}$
所以:$M=\frac{{4{π^2}{r^3}}}{{G{T^2}}}=\frac{s^2}{{G{t^2}θ}}$.故C正确;
D、人造航天器在月球表面上空绕月球做匀速圆周运动,月球的半径等于r,则月球的体积:V=$\frac{4}{3}$πr3,月球的密度为:$ρ=\frac{M}{V}=\frac{{3{θ^2}}}{{4G{t^2}}}$.故D正确.
故选:BCD
点评 万有引力在天体中的运动,主要是万有引力充当向心力,注意向心力的表达有多种形式,应灵活选择.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
3. 如图所示,电路电压U保持不变,滑动变阻器R的总阻值与R2的阻值均为20Ω,电阻R1的阻值为5Ω当滑动变阻器R的滑动端P由a向b滑动过程中( )
如图所示,电路电压U保持不变,滑动变阻器R的总阻值与R2的阻值均为20Ω,电阻R1的阻值为5Ω当滑动变阻器R的滑动端P由a向b滑动过程中( )
 如图所示,电路电压U保持不变,滑动变阻器R的总阻值与R2的阻值均为20Ω,电阻R1的阻值为5Ω当滑动变阻器R的滑动端P由a向b滑动过程中( )
如图所示,电路电压U保持不变,滑动变阻器R的总阻值与R2的阻值均为20Ω,电阻R1的阻值为5Ω当滑动变阻器R的滑动端P由a向b滑动过程中( )| A. | 干路中电流不断增大 | B. | R1上消耗的电功率不断增大 | ||
| C. | R1上消耗的电功率不断减小 | D. | R2上消耗的电功率不断减小 |
11.物体在水平拉力F作用下,沿x轴方向由坐标原点开始运动,设拉力F随x的变化分别如图甲、乙、丙所示,其中图甲为一半圆图形,对应拉力做功分别为W1、W2、W3,则以下说法正确的是( )
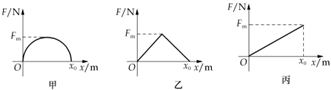

| A. | W1>W2>W3 | B. | W1>W2=W3 | ||
| C. | W1=W2=W3 | D. | 无法比较它们的大小 |
15.若宇航员在月球表面附近自高h处以初速度v0水平抛出一个小球,测出小球的水平射程为L.已知月球半径为R,万有引力常量为G.则下列说法正确的是( )
| A. | 月球表面的重力加速度g月=$\frac{h{v}_{0}^{2}}{{L}^{2}}$ | |
| B. | 月球的平均密度ρ=$\frac{3h{v}_{0}^{2}}{2πG{L}^{2}R}$ | |
| C. | 月球的第一宇宙速度v=$\frac{{v}_{0}}{L}$$\sqrt{2h}$ | |
| D. | 月球的质量m月=$\frac{h{R}^{2}{v}_{0}^{2}}{G{L}^{2}}$ |
10.两个质量相等的球形物体,两球心相距r,它们之间的万有引力为F,若它们的质量都加倍,两球心间的距离也加倍,则它们之间的作用力为原来的( )
| A. | 0.5倍 | B. | 1倍 | C. | 0.25倍 | D. | 4倍 |
 黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成.两星视为质点,不考虑其它天体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图所示.引力常量为G,由观测能够得到可见星A的速率v和运行周期T.
黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成.两星视为质点,不考虑其它天体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图所示.引力常量为G,由观测能够得到可见星A的速率v和运行周期T.