题目内容
1. 如图所示,完全相同的甲乙丙三个小球,分别从倾角为60°、45°、30°的光滑斜面的顶端由静止滑下,下列说法正确的是( )
如图所示,完全相同的甲乙丙三个小球,分别从倾角为60°、45°、30°的光滑斜面的顶端由静止滑下,下列说法正确的是( )| A. | 甲乙下滑时间相等 | B. | 甲丙下滑时间相等 | ||
| C. | 乙丙下滑时间相等 | D. | 甲乙丙下滑时间均不相等 |
分析 根据牛顿第二定律求出小球的加速度,根据位移时间公式求出时间的表达式,从而比较运动的时间.
解答 解:设斜面与水平面的倾角为θ,根据牛顿第二定律得,加速度a=$\frac{mgsinθ}{m}=gsinθ$,
设底边的长度为d,则斜面的长度s=$\frac{d}{cosθ}$,
根据s=$\frac{1}{2}a{t}^{2}$得,t=$\sqrt{\frac{2s}{a}}=\sqrt{\frac{2d}{gsinθcosθ}}=\sqrt{\frac{4d}{gsin2θ}}$,
可知θ=60°和30°时,t相等,即甲丙的时间相等,与乙的时间不等,故B正确,A、C、D错误.
故选:B.
点评 本题考查了牛顿第二定律和运动学公式的基本运用,知道加速度是联系力学和运动学的桥梁.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
8. 如图所示,P是主动轮,通过皮带带动从动轮Q转动,A和B、C和D分别是皮带轮边缘相互接触的点,如果皮带不打滑,则( )
如图所示,P是主动轮,通过皮带带动从动轮Q转动,A和B、C和D分别是皮带轮边缘相互接触的点,如果皮带不打滑,则( )
 如图所示,P是主动轮,通过皮带带动从动轮Q转动,A和B、C和D分别是皮带轮边缘相互接触的点,如果皮带不打滑,则( )
如图所示,P是主动轮,通过皮带带动从动轮Q转动,A和B、C和D分别是皮带轮边缘相互接触的点,如果皮带不打滑,则( )| A. | A和B、C和D处于相对静止状态 | |
| B. | B点相对A点运动趋势的方向与B点运动方向相反 | |
| C. | D点受到摩擦力的方向与D点的运动方向相同 | |
| D. | A点受到摩擦力的方向与A点的运动方向相同 |
12. 如图所示电路中,电源内阻不可忽略,A、B两灯电阻分别为R和4R.滑动变阻器的滑片移动到上下电阻2:1的位置,两灯功率相同,当将滑片移动到最上端,则( )
如图所示电路中,电源内阻不可忽略,A、B两灯电阻分别为R和4R.滑动变阻器的滑片移动到上下电阻2:1的位置,两灯功率相同,当将滑片移动到最上端,则( )
 如图所示电路中,电源内阻不可忽略,A、B两灯电阻分别为R和4R.滑动变阻器的滑片移动到上下电阻2:1的位置,两灯功率相同,当将滑片移动到最上端,则( )
如图所示电路中,电源内阻不可忽略,A、B两灯电阻分别为R和4R.滑动变阻器的滑片移动到上下电阻2:1的位置,两灯功率相同,当将滑片移动到最上端,则( )| A. | A灯变亮,B灯变暗 | B. | A灯变暗,B灯变亮 | ||
| C. | A灯得功率可能为原来的$\frac{1}{2}$ | D. | A灯得功率可能为原来的$\frac{3}{4}$ |
9.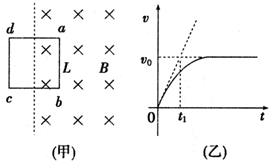 一有界匀强磁场区域如图(甲)所示,abcd是一个质量为m、电阻为R、边长为L、匝数为N的正方形线圈.线圈一半在磁场内,一半在磁场外.t=0时刻磁场磁感应强度由B0开始均匀减小,线圈在磁场力作用下运动,v-t图象如图(乙),图中斜向虚线为速度图线在0点的切线,数据由图中给出,不考虑重力影响.则磁场磁感应强度的变化率为( )
一有界匀强磁场区域如图(甲)所示,abcd是一个质量为m、电阻为R、边长为L、匝数为N的正方形线圈.线圈一半在磁场内,一半在磁场外.t=0时刻磁场磁感应强度由B0开始均匀减小,线圈在磁场力作用下运动,v-t图象如图(乙),图中斜向虚线为速度图线在0点的切线,数据由图中给出,不考虑重力影响.则磁场磁感应强度的变化率为( )
 一有界匀强磁场区域如图(甲)所示,abcd是一个质量为m、电阻为R、边长为L、匝数为N的正方形线圈.线圈一半在磁场内,一半在磁场外.t=0时刻磁场磁感应强度由B0开始均匀减小,线圈在磁场力作用下运动,v-t图象如图(乙),图中斜向虚线为速度图线在0点的切线,数据由图中给出,不考虑重力影响.则磁场磁感应强度的变化率为( )
一有界匀强磁场区域如图(甲)所示,abcd是一个质量为m、电阻为R、边长为L、匝数为N的正方形线圈.线圈一半在磁场内,一半在磁场外.t=0时刻磁场磁感应强度由B0开始均匀减小,线圈在磁场力作用下运动,v-t图象如图(乙),图中斜向虚线为速度图线在0点的切线,数据由图中给出,不考虑重力影响.则磁场磁感应强度的变化率为( )| A. | $\frac{mR{v}_{0}}{{t}_{1}N{B}_{0}{L}^{3}}$ | B. | $\frac{2mR{v}_{0}}{{t}_{1}N{B}_{0}{L}^{2}}$ | ||
| C. | $\frac{mR{v}_{0}}{{t}_{1}{N}^{2}{B}_{0}{L}^{2}}$ | D. | $\frac{2mR{v}_{0}}{{t}_{1}{N}^{2}{B}_{0}{L}^{3}}$ |
16. 11月28日阿联酋迪拜成功获得了2020年世博会的举办权,人们在世界最高建筑哈利法塔(原名迪拜塔,高828m)上庆祝申办成功.假设塔内有一部电梯某次运送乘客的速度-时间图象如图所示,下列判断正确的是( )
11月28日阿联酋迪拜成功获得了2020年世博会的举办权,人们在世界最高建筑哈利法塔(原名迪拜塔,高828m)上庆祝申办成功.假设塔内有一部电梯某次运送乘客的速度-时间图象如图所示,下列判断正确的是( )
 11月28日阿联酋迪拜成功获得了2020年世博会的举办权,人们在世界最高建筑哈利法塔(原名迪拜塔,高828m)上庆祝申办成功.假设塔内有一部电梯某次运送乘客的速度-时间图象如图所示,下列判断正确的是( )
11月28日阿联酋迪拜成功获得了2020年世博会的举办权,人们在世界最高建筑哈利法塔(原名迪拜塔,高828m)上庆祝申办成功.假设塔内有一部电梯某次运送乘客的速度-时间图象如图所示,下列判断正确的是( )| A. | 该图象一定是电梯上行图象 | B. | 0~3s电梯的位移为45m | ||
| C. | 从出发到停止电梯的位移为450m | D. | 全过程中合外力对电梯做的功为零 |
13.如图所示,表示横波在某一时刻的图象,其波速是8m/s,则下列说法中正确的是( )

| A. | 该波的周期为1s | |
| B. | 此刻质点a的振动方向向上 | |
| C. | 从这一时刻开始经过1.75s,质点a经过的路程是70cm | |
| D. | 从这一时刻开始经过2.0s,质点a向右移动的距离为16m |
10. 质量为M的皮带轮工件放置在水平桌面上,一细绳绕过皮带轮的皮带槽,一端系一质量为m的重物,另一端固定在桌面上.如图所示,工件与桌面、绳之间以及绳与桌面边缘之间的摩擦都忽略不计,桌面上绳子与桌面平行,则重物下落过程中,工件的加速度为( )
质量为M的皮带轮工件放置在水平桌面上,一细绳绕过皮带轮的皮带槽,一端系一质量为m的重物,另一端固定在桌面上.如图所示,工件与桌面、绳之间以及绳与桌面边缘之间的摩擦都忽略不计,桌面上绳子与桌面平行,则重物下落过程中,工件的加速度为( )
 质量为M的皮带轮工件放置在水平桌面上,一细绳绕过皮带轮的皮带槽,一端系一质量为m的重物,另一端固定在桌面上.如图所示,工件与桌面、绳之间以及绳与桌面边缘之间的摩擦都忽略不计,桌面上绳子与桌面平行,则重物下落过程中,工件的加速度为( )
质量为M的皮带轮工件放置在水平桌面上,一细绳绕过皮带轮的皮带槽,一端系一质量为m的重物,另一端固定在桌面上.如图所示,工件与桌面、绳之间以及绳与桌面边缘之间的摩擦都忽略不计,桌面上绳子与桌面平行,则重物下落过程中,工件的加速度为( )| A. | $\frac{2mg}{M+4m}$ | B. | $\frac{2mg}{M+2m}$ | C. | $\frac{mg}{2M}$ | D. | $\frac{mg}{M+m}$ |



