题目内容
15.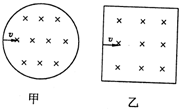 如图甲、乙是场强相同的圆形、正方形匀强磁场区域(圆形直径与正方形边长相同).不计重力的相同带电粒子以相同速度沿垂直于磁场方向飞入两个磁场区域,进入圆形磁场的粒子初速度方向对准圆心,进入正方形磁场的粒子初速度方向垂直于边界且从中点进入,则粒子分别经过两个磁场区域后,其速度变化△v甲、△v乙的大小关系为( )
如图甲、乙是场强相同的圆形、正方形匀强磁场区域(圆形直径与正方形边长相同).不计重力的相同带电粒子以相同速度沿垂直于磁场方向飞入两个磁场区域,进入圆形磁场的粒子初速度方向对准圆心,进入正方形磁场的粒子初速度方向垂直于边界且从中点进入,则粒子分别经过两个磁场区域后,其速度变化△v甲、△v乙的大小关系为( )| A. | △v甲<△v乙 | B. | △v甲>△v乙 | C. | △v甲≤△v乙 | D. | △v甲≥△v乙 |
分析 带电粒子垂直于磁场方向进入匀强磁场,洛伦兹力提供向心力,由牛顿第二定律得到轨道半径表达式,结合条件,分析半径关系;运动时间的判断可以根据转过的圆心角的大小;比较哪个磁场粒子先出磁场,可以做出多个轨迹比较.
解答 解:带电粒子垂直于磁场方向进入匀强磁场,洛伦兹力提供向心力,由qvB=m$\frac{{v}^{2}}{r}$,解得两个带电粒子在磁场中运动的轨道半径r=$\frac{mv}{qB}$.由题可得,两个带电粒子在磁场中运动的半径一定相同.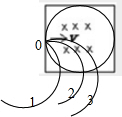 带电粒子在匀强磁场中运动周期 T=$\frac{2πm}{qB}$.
带电粒子在匀强磁场中运动周期 T=$\frac{2πm}{qB}$.
设正方形的边长为L.若带电粒子的比荷相同且在匀强磁场中运动的轨道半径满足r=$\frac{1}{2}$L,则两个带电粒子在匀强磁场中运动时间均为$\frac{1}{4}$周期,两个带电粒子在磁场中运动的时间相同,则根据平行四边形定则可得速度变化的大小均△v=$\sqrt{2}$v.即△v甲=△v乙.
若r≠$\frac{1}{2}$L,画出两个带电粒子在匀强磁场中的可能轨迹示意图,显然进入圆形区域的带电粒子轨迹所对的圆心角一定小于进入正方形区域的带电粒子轨迹所对的圆心角,此时有△v甲<△v乙.所以有△v甲≤△v乙.
故选:C.
点评 本题的关键在于在同一个图象中做出多个轨迹进行比较,运用平行四边形定则或三角形定则分析.

练习册系列答案
相关题目
6.以下关于电场和电场线的说法中正确的是( )
| A. | 同一试探电荷在电场线密集的地方所受电场力大 | |
| B. | 电场线不仅能在空间相交,也能相切 | |
| C. | 越靠近正点电荷,电场线越密,电场强度越大,越靠近负点电荷,电场线越稀,电场强度越小 | |
| D. | 电场线是人们假想的,用以表示电场的强弱和方向,和电场一样实际并不存在 |
3. 如图所示,楔形物体B静止在粗糙的斜面上,其质量为M,斜面倾角为θ.一质量为m的小物块A静止在斜面上.用恒力F沿斜面向上拉小物块,小物体A仍然静止在斜面上.下列说法正确的是( )
如图所示,楔形物体B静止在粗糙的斜面上,其质量为M,斜面倾角为θ.一质量为m的小物块A静止在斜面上.用恒力F沿斜面向上拉小物块,小物体A仍然静止在斜面上.下列说法正确的是( )
 如图所示,楔形物体B静止在粗糙的斜面上,其质量为M,斜面倾角为θ.一质量为m的小物块A静止在斜面上.用恒力F沿斜面向上拉小物块,小物体A仍然静止在斜面上.下列说法正确的是( )
如图所示,楔形物体B静止在粗糙的斜面上,其质量为M,斜面倾角为θ.一质量为m的小物块A静止在斜面上.用恒力F沿斜面向上拉小物块,小物体A仍然静止在斜面上.下列说法正确的是( )| A. | 没有施加恒力F耐,地面对楔形物体B的支持力为Mg | |
| B. | 没有施加恒力F时,地面对楔形物体B的摩擦力为mgcosθ | |
| C. | 施加恒力F时,地面对楔形物体B的支持力为(M+m)g | |
| D. | 施加恒力F时,地面对楔形物体B的摩擦力为Fcosθ |
6.有一条两岸平直、河水均匀流动、流速恒定的河流,小强驾着小船渡河,去程时行驶路线与河岸垂直,回程时船头指向始终与河岸垂直.去程与回程所用时间的比值为k,若船在静水中的速度大小为v,则河水流速为( )
| A. | $\frac{\sqrt{{k}^{2}-1}}{k}$v | B. | v$\sqrt{1-{k}^{2}}$ | C. | v$\sqrt{{k}^{2}+1}$ | D. | $\frac{\sqrt{1+{k}^{2}}}{k}$v |
4. 一列简谐横波在t=0时刻的波形如图所示,质点P此时刻沿-y方向运动,经过0.2s第一次回到平衡位置,则( )
一列简谐横波在t=0时刻的波形如图所示,质点P此时刻沿-y方向运动,经过0.2s第一次回到平衡位置,则( )
 一列简谐横波在t=0时刻的波形如图所示,质点P此时刻沿-y方向运动,经过0.2s第一次回到平衡位置,则( )
一列简谐横波在t=0时刻的波形如图所示,质点P此时刻沿-y方向运动,经过0.2s第一次回到平衡位置,则( )| A. | 该波沿x轴正方向传播 | B. | 波的周期为0.2s | ||
| C. | 波的传播速度为30m/s | D. | 质点Q的振动方程为y=5cos5πt(cm) |
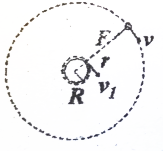 已知地球半径R,地球表面重力加速度g.卫星m绕地球做圆周运动,轨道半径为r.求:
已知地球半径R,地球表面重力加速度g.卫星m绕地球做圆周运动,轨道半径为r.求:

 滑块A、B沿光滑水平面上同一条直线发生碰撞;碰撞后两者粘在一起运动;两者的位置x随时间t变化的图象如图所示.求:
滑块A、B沿光滑水平面上同一条直线发生碰撞;碰撞后两者粘在一起运动;两者的位置x随时间t变化的图象如图所示.求: