题目内容
17. 如图所示,一个长L=1m,质量M=2kg的长木板A,静止的放在光滑水平面上,A的左端放置一个光滑的小滑块B,B可视为质点,其质量m=1kg,今有一个质量也为m=1kg的滑块C,以v=3m/s的速度沿水平面向左匀速运动与A发生碰撞,碰撞中机械能损失不计.求:
如图所示,一个长L=1m,质量M=2kg的长木板A,静止的放在光滑水平面上,A的左端放置一个光滑的小滑块B,B可视为质点,其质量m=1kg,今有一个质量也为m=1kg的滑块C,以v=3m/s的速度沿水平面向左匀速运动与A发生碰撞,碰撞中机械能损失不计.求:(1)碰后A和C的速度大小和方向;
(2)碰后B在A上运动的时间.
分析 (1)AC碰撞中机械能损失不计,由动量守恒定律和机械能守恒定律列式,求碰后A和C的速度大小和方向.
(2)AC碰后B静止不动,根据匀速运动的规律求B在A上运动时间.
解答 解:(1)AC相碰过程中,取向左为正方向,由动量守恒定律得
mv=MvA+mvC;
由机械能守恒定律得
$\frac{1}{2}$mv2=$\frac{1}{2}$MvA2+$\frac{1}{2}$mvC2;
解得 vA=$\frac{2m}{M+m}$v=2m/s,方向向左
vC=$\frac{m-M}{m+M}$v=-1m/s,方向向右
(2)AC碰后B静止不动,B在A上运动时间为
t=$\frac{L}{{v}_{A}}$=0.5s
答:
(1)碰后A的速度大小是2m/s,方向向左.C的速度大小是1m/s,方向向右;
(2)碰后B在A上运动的时间是0.5s.
点评 本题中AC发生的是弹性碰撞,遵守动量守恒定律和机械能守恒定律,列式时要注意选取正方向,用正负号表示速度的方向.

练习册系列答案
相关题目
9.汽车正在以12m/s的速度在平直的公路上前进,在它的正前方15m处有一障碍物,汽车立即刹车做匀减速运动,加速度大小为6m/s2,刹车后3s末汽车和障碍物之间的距离为( )
| A. | 3 m | B. | 6 m | C. | 12 m | D. | 9 m |
12. 在如图所示的电路中,电源电动势为12V,电源内阻为1.0Ω,电路中的电阻R0为1.5Ω,小型直流电动机M的内阻为0.5Ω.闭合开关S后,电动机转动,电流表的示数为2.0A.以下判断正确的是( )
在如图所示的电路中,电源电动势为12V,电源内阻为1.0Ω,电路中的电阻R0为1.5Ω,小型直流电动机M的内阻为0.5Ω.闭合开关S后,电动机转动,电流表的示数为2.0A.以下判断正确的是( )
 在如图所示的电路中,电源电动势为12V,电源内阻为1.0Ω,电路中的电阻R0为1.5Ω,小型直流电动机M的内阻为0.5Ω.闭合开关S后,电动机转动,电流表的示数为2.0A.以下判断正确的是( )
在如图所示的电路中,电源电动势为12V,电源内阻为1.0Ω,电路中的电阻R0为1.5Ω,小型直流电动机M的内阻为0.5Ω.闭合开关S后,电动机转动,电流表的示数为2.0A.以下判断正确的是( )| A. | 电动机两端的电压为1.0V | B. | 电动机输出的机械功率为12W | ||
| C. | 电动机内阻的热功率为2.0W | D. | 电源输出的功率为24W |
2. 我国预计于2017年前后发射嫦娥五号,实现月球取样并返回地球,根据目前的设计方案,嫦娥五号由轨道器、着陆器等多个部分组成,着陆器携带样品从月球表面升空,先在近月圆轨道Ⅰ上运行,经轨道调整后与较高轨道Ⅱ上的轨道器对接,最后由轨道器携带样品返回地球,下列关于此过程中说法正确的是( )
我国预计于2017年前后发射嫦娥五号,实现月球取样并返回地球,根据目前的设计方案,嫦娥五号由轨道器、着陆器等多个部分组成,着陆器携带样品从月球表面升空,先在近月圆轨道Ⅰ上运行,经轨道调整后与较高轨道Ⅱ上的轨道器对接,最后由轨道器携带样品返回地球,下列关于此过程中说法正确的是( )
 我国预计于2017年前后发射嫦娥五号,实现月球取样并返回地球,根据目前的设计方案,嫦娥五号由轨道器、着陆器等多个部分组成,着陆器携带样品从月球表面升空,先在近月圆轨道Ⅰ上运行,经轨道调整后与较高轨道Ⅱ上的轨道器对接,最后由轨道器携带样品返回地球,下列关于此过程中说法正确的是( )
我国预计于2017年前后发射嫦娥五号,实现月球取样并返回地球,根据目前的设计方案,嫦娥五号由轨道器、着陆器等多个部分组成,着陆器携带样品从月球表面升空,先在近月圆轨道Ⅰ上运行,经轨道调整后与较高轨道Ⅱ上的轨道器对接,最后由轨道器携带样品返回地球,下列关于此过程中说法正确的是( )| A. | 着陆器在Ⅱ轨道的动能必定大于Ⅰ轨道的动能 | |
| B. | 着陆器在Ⅰ轨道的机械能小于在Ⅱ轨道的机械能 | |
| C. | 着陆器应通过减速到达Ⅱ轨道从而实现与轨道器对接 | |
| D. | 着陆器应先到达Ⅱ轨道,然后向前加速度加速,即可追上轨道器实现对接 |
9.两个互相垂直的力F1和F2同时作用在同一物体上,使物体由静止开始运动,物体通过一段位移的过程中,力F1对物体做功为8J,力F2对物体做功为6J,则F1和F2的合力对物体做功为( )
| A. | 2J | B. | 7J | C. | 10J | D. | 14J |
6.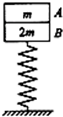 如图所示,A、B的质量分别为m,2m,叠放在轻质弹簧上(弹簧下端固定于地面上),对A施加一竖直向下、大小为F(F>3mg)的力,将弹簧再压缩一段距离(始终在弹性限度内)而处于平衡状态,现突然撤去F,设两物体向上运动的过程中A、B间相互作用力大小为FN,则关于FN的说法中正确的是(重力加速度为g)( )
如图所示,A、B的质量分别为m,2m,叠放在轻质弹簧上(弹簧下端固定于地面上),对A施加一竖直向下、大小为F(F>3mg)的力,将弹簧再压缩一段距离(始终在弹性限度内)而处于平衡状态,现突然撤去F,设两物体向上运动的过程中A、B间相互作用力大小为FN,则关于FN的说法中正确的是(重力加速度为g)( )
 如图所示,A、B的质量分别为m,2m,叠放在轻质弹簧上(弹簧下端固定于地面上),对A施加一竖直向下、大小为F(F>3mg)的力,将弹簧再压缩一段距离(始终在弹性限度内)而处于平衡状态,现突然撤去F,设两物体向上运动的过程中A、B间相互作用力大小为FN,则关于FN的说法中正确的是(重力加速度为g)( )
如图所示,A、B的质量分别为m,2m,叠放在轻质弹簧上(弹簧下端固定于地面上),对A施加一竖直向下、大小为F(F>3mg)的力,将弹簧再压缩一段距离(始终在弹性限度内)而处于平衡状态,现突然撤去F,设两物体向上运动的过程中A、B间相互作用力大小为FN,则关于FN的说法中正确的是(重力加速度为g)( )| A. | 刚撤去外力F时,FN=$\frac{F+mg}{3}$ | B. | 弹簧弹力等于F时,FN=$\frac{F}{3}$ | ||
| C. | 当两物体速度最大时,FN=mg | D. | 当弹簧恢复原长时,FN=0 |
14.如图所示为一交流电的电流随时间变化的图象,则此交流电的有效值为( )


| A. | 3A | B. | 4A | C. | 5A | D. | 6A |
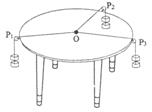 用如下的器材和方法可以验证“力的平行四边形定则“.在圆形桌子透明桌面上平铺一张白纸,在桌子边缘安装三个光滑的滑轮,其中,滑轮P1固定在桌子边,滑轮P2、P3可沿桌边移动.第一次实验中,步骤如下:
用如下的器材和方法可以验证“力的平行四边形定则“.在圆形桌子透明桌面上平铺一张白纸,在桌子边缘安装三个光滑的滑轮,其中,滑轮P1固定在桌子边,滑轮P2、P3可沿桌边移动.第一次实验中,步骤如下: