题目内容
17．
如图所示，一铁球用一轻绳悬挂于O点，用力F拉住小球，要使轻绳与竖直方向保持66°角不变，且F最小，则F与竖直方向的夹角θ应为（ ）| A． | 90° | B． | 66° | C． | 24° | D． | 0° |
分析 小球始终处于平衡状态，合力为零，根据共点力平衡，抓住重力不变，细绳的拉力方向不变，运用作图法求出F有最小值时的θ值．
解答 
解：如图所示，小球受三个力而处于平衡状态，重力mg的大小和方向都不变，绳子拉力T方向不变，因为绳子拉力T和外力F的合力等于重力，通过作图法知，当F的方向与绳子方向垂直时，由于垂线段最短，所以F最小，则由几何知识得θ=90°-66°=24°．故C正确，A、B、D错误．
故选：C．
点评 本题属于力学的动态分析，关键能够正确进行受力分析，抓住不变量，运用作图法进行求解．
练习册系列答案
相关题目
14．
如图所示，重为G的物体静止在水平地面上，此时物体对地面的压力等于重力G，如果选择下列规律中的某个中几个作为依据来证明 上述结论，最为合适的一项是（ ）
①牛顿第一定律 ②牛顿第二定律 ③牛顿第三定律．
如图所示，重为G的物体静止在水平地面上，此时物体对地面的压力等于重力G，如果选择下列规律中的某个中几个作为依据来证明 上述结论，最为合适的一项是（ ）①牛顿第一定律 ②牛顿第二定律 ③牛顿第三定律．
| A． | ① | B． | ①② | C． | ③ | D． | ②③ |
8．
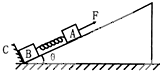在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B，它们的质量分别为m1、m2，弹簧劲度系数为k，C为一固定挡板，系统处于静止状态．现用一平行于斜面向上的恒力F拉物块A使之向上运动，当物块B刚要离开挡板C时，物块A沿斜面运动的距离为d，速度为v，此时（ ）
在倾角为θ的固定光滑斜面上有两个用轻弹簧相连接的物块A、B，它们的质量分别为m1、m2，弹簧劲度系数为k，C为一固定挡板，系统处于静止状态．现用一平行于斜面向上的恒力F拉物块A使之向上运动，当物块B刚要离开挡板C时，物块A沿斜面运动的距离为d，速度为v，此时（ ）| A． | 拉力F做功的等于A动能的增加量 | |
| B． | 物块B满足m2gsinθ=kd | |
| C． | 物块A的加速度为$\frac{F-kd}{{m}_{1}}$ | |
| D． | 弹簧弹性势能的增加量为Fd-m1gdsinθ-$\frac{1}{2}$m1v2 |
5．质量为m的物体竖直下落，重力加速度为g．从静止到速度为v的过程中，重力的平均功率为（ ）
| A． | mv | B． | mgv | C． | $\frac{1}{2}$mv2 | D． | $\frac{1}{2}$mgv |
12．
如图所示，质量为M的斜面体A放在粗糙水平面上，用轻绳拴住质量为m的小球B置于斜面上，轻绳与斜面平行且另一端固定在竖直墙面上，不计小球与斜面间的摩擦，斜面体与墙不接触，整个系统处于静止状态．则（ ）
如图所示，质量为M的斜面体A放在粗糙水平面上，用轻绳拴住质量为m的小球B置于斜面上，轻绳与斜面平行且另一端固定在竖直墙面上，不计小球与斜面间的摩擦，斜面体与墙不接触，整个系统处于静止状态．则（ ）| A． | 斜面体对水平面的压力等于（M+m）g | |
| B． | 水平面对斜面体有向左的摩擦力作用 | |
| C． | 当滑块缓慢向右移动时，斜面对小球的支持力变大 | |
| D． | 当滑块缓慢向右移动时，细线对小球的拉力先变小 |
2．对于库仑定律，下面说法正确的是（ ）
| A． | 库仑定律适用于真空中两个点电荷之间的相互作用力 | |
| B． | 两个带电小球即使相距非常近，也能用库仑定律 | |
| C． | 相互作用的两个点电荷，不论它们的电荷量是否相同，它们之间的库仑力大小一定相等 | |
| D． | 两个点电荷的电量各减为原来的一半，它们之间的距离保持不变，则它们之间库存仑力减为原来的一半 |
9．
真空中三维坐标系Oxyz的z轴方向竖直向上，在坐标原点0上固定一带正电的点电荷Q，其形成的电场如图所示，一重力不能忽略的带电微粒q正在该点电荷附近做匀速圆周运动．则（ ）
真空中三维坐标系Oxyz的z轴方向竖直向上，在坐标原点0上固定一带正电的点电荷Q，其形成的电场如图所示，一重力不能忽略的带电微粒q正在该点电荷附近做匀速圆周运动．则（ ）| A． | 该微粒带负电，轨道圆心在坐标原点O上 | |
| B． | 该微粒带负电，轨道圆心在z轴的负半轴上某一点 | |
| C． | 该微粒带正电，轨道圆心在坐标原点0上 | |
| D． | 该微粒带正电，轨道圆心在z轴的正半轴上某一点 |