题目内容
19.我国发射了一颗绕月运行的探月卫星“嫦娥一号”.设该卫星的轨道是圆形的,且贴近月球表面.已知月球的质量约为地球质量的$\frac{1}{81}$,月球的半径约为地球半径的$\frac{1}{4}$,地球上的第一宇宙速度约为7.9km/s,则该探月卫星绕月球表面运行的速率约为1.8 km/s 月球表面的重力加速度为地球表面的重力加速度的$\frac{16}{81}$倍.分析 (1)根据万有引力提供向心力,求出速度与轨道半径的关系,从而得出探月卫星的速度与地球第一宇宙速度的关系.
(2)根据万有引力等于重力得出表面重力加速度与中心天体半径和质量的关系,从而通过地球表面的重力加速度求出月球表面的重力加速度.
解答 解:根据万有引力提供向心力得:
$\frac{GMm}{{R}^{2}}$=m$\frac{{v}^{2}}{R}$
解得:v=$\sqrt{\frac{GM}{R}}$,
已知月球的质量约为地球质量的$\frac{1}{81}$,月球的半径约为地球半径的$\frac{1}{4}$,
所以地球上的第一宇宙速度是月球上的第一宇宙速度的$\frac{9}{2}$倍.
地球上的第一宇宙速度约为7.9km/s,则该探月卫星绕月球表面运行的速率约为:v=1.8km/s,
根据万有引力等于重力得:
$\frac{GMm}{{R}^{2}}$=mg,
g=$\frac{GM}{{R}^{2}}$,已知月球的质量约为地球质量的$\frac{1}{81}$,月球的半径约为地球半径的$\frac{1}{4}$,
所以月球表面的重力加速度为地球表面的重力加速度的$\frac{16}{81}$倍.
故答案为:1.8,$\frac{16}{81}$
点评 解决本题的关键掌握万有引力等于重力和万有引力提供向心力这两个理论,并能熟练运用.

练习册系列答案
 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
10.木星公转周期约为12年,地球到太阳的距离为1天文单位,则木星到太阳的距离最接近( )
| A. | 5天文单位 | B. | 12天文单位 | C. | 2天文单位 | D. | 4天文单位 |
7.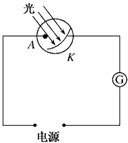 如图所示电路的全部接线及元件均完好.用光照射光电管的K极板,发现电流计无电流通过,可能的原因是( )
如图所示电路的全部接线及元件均完好.用光照射光电管的K极板,发现电流计无电流通过,可能的原因是( )
 如图所示电路的全部接线及元件均完好.用光照射光电管的K极板,发现电流计无电流通过,可能的原因是( )
如图所示电路的全部接线及元件均完好.用光照射光电管的K极板,发现电流计无电流通过,可能的原因是( )| A. | A、K间加的电压不够高 | B. | 电源正负极接反了 | ||
| C. | 照射光的强度不够大 | D. | 照射光的频率不够高 |
14.如图所示小物体A与圆盘保持相对静止跟着圆盘一起做匀速圆周运动,则下列说法正确的是( )
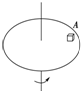

| A. | 木块受到圆盘对它的静摩擦力,方向指向圆盘中心 | |
| B. | 由于木块相对圆盘静止,所以不受摩擦力 | |
| C. | 由于木块运动,所以受到滑动摩擦力 | |
| D. | 由于木块做匀速圆周运动,所以,除了受到重力、支持力、摩擦力外,还受向心力 |
4.关于合运动和分运动,下列说法不正确的是( )
| A. | 合运动和分运动的时间相同 | |
| B. | 由合运动分解为两个分运动,可以有两个不同的分解方法 | |
| C. | 物体做曲线运动时,才能将这个运动分解为两个分运动 | |
| D. | 任何形式的运动,都可以用几个分运动代替 |
11.川师附中建设新的体育馆,需要用起重机把建筑材料运送到高处,一起重机的钢绳由静止开始匀加速提起质量为m的建筑材料,当重物的速度为v1时,起重机的有用功率达到最大值P,此后,起重机保持该功率不变,继续提升重物,直到以最大速度v2匀速上升为止,物体上升的高度为h,则整个过程中,下列说法正确的是( )
| A. | 钢绳的最大拉力为$\frac{P}{v_2}$ | B. | 钢绳的最大拉力为$\frac{P}{v_1}$ | ||
| C. | 重物的匀加速最大速度v1=$\frac{P}{mg}$ | D. | 起重机对重物做的功为mgh+$\frac{1}{2}$mv22 |
8.原子的质量主要集中在( )
| A. | 质子上 | B. | 中子上 | C. | 电子上 | D. | 原子核上 |