题目内容
1.卫星绕地球做匀速圆周运动,速度越大的卫星( )| A. | 半径一定越大 | B. | 周期一定越大 | C. | 向心力一定越大 | D. | 加速度一定越大 |
分析 根据万有引力提供向心力,先根据线速度关系分析半径关系,再分析向心加速度、周期与轨道半径之间存在什么关系.
解答 解:A、根据万有引力提供向心力得:$G\frac{Mm}{{r}^{2}}=m\frac{{v}^{2}}{r}$,解得:v=$\sqrt{\frac{GM}{r}}$,则速度越大,半径越小,故A错误;
B、根据$G\frac{Mm}{{r}^{2}}=m\frac{4{π}^{2}r}{{T}^{2}}$得:T=$2π\sqrt{\frac{{r}^{3}}{GM}}$,半径越小,周期越小,故B错误;
C、向心力F=$G\frac{Mm}{{r}^{2}}$,由于不知道卫星质量关系,所以无法判断向心力大小,故C错误;
D、根据$G\frac{Mm}{{r}^{2}}=ma$,得a=$G\frac{M}{{r}^{2}}$,半径越小,加速度越大,故D正确;
故选:D
点评 解决本题的关键利用万有引力提供向心力这一知识点,特别注意不能比较向心力的大小,难度适中.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
11.光在科学技术、生产和生活中有着广泛的应用,下列符合实际应用的是( )
| A. | 在光导纤维束内传送图象是利用光的色散现象 | |
| B. | 用透明的标准平面样板检查光学平面的平整程度是利用光的衍射现象 | |
| C. | 光学镜头上的增透膜是利用光的干涉现象 | |
| D. | 各种光均会发生偏振现象 |
9.物体在下列运动过程中,机械能守恒的是( )
| A. | 沿粗糙斜面匀速下滑 | B. | 沿粗糙斜面匀速上滑 | ||
| C. | 沿粗糙斜面加速下滑 | D. | 沿光滑斜面自由下滑 |
6. 如图所示,一个圆盘在水平面内匀速转动,盘面上距圆盘中心一定距离处放有一个小木块随圆盘一起转动,木块受哪些力作用( )
如图所示,一个圆盘在水平面内匀速转动,盘面上距圆盘中心一定距离处放有一个小木块随圆盘一起转动,木块受哪些力作用( )
 如图所示,一个圆盘在水平面内匀速转动,盘面上距圆盘中心一定距离处放有一个小木块随圆盘一起转动,木块受哪些力作用( )
如图所示,一个圆盘在水平面内匀速转动,盘面上距圆盘中心一定距离处放有一个小木块随圆盘一起转动,木块受哪些力作用( )| A. | 木块受重力、圆盘的支持力和向心力 | |
| B. | 圆盘对木块的支持力、静摩擦力和重力 | |
| C. | 圆盘对木块的静摩擦力、支持力和重力以及向心力作用 | |
| D. | 圆盘对木块的支持力和静摩擦 |
11.爱因斯坦曾把一代代物理学家探索自然奥秘的努力比作福尔摩斯侦探小说中的警员破案.下列说法符合物理史实的是( )
| A. | 著名物理学家伽利略首先指出,如果运动中的物体没有受到力的作用,它将继续以同一速度沿同一直线运动,既不停下来也不偏离原来的方向 | |
| B. | 伽利略研究落体运动时,将落体实验转化为斜面实验,冲淡了重力的作用,便于小球运动路程的测量 | |
| C. | 科学巨人牛顿在伽利略和笛卡儿的工作基础上,提出了动力学的一条基本定律,那就是惯性定律 | |
| D. | 安培通过研究电磁感应现象得出了安培定则,法拉第电磁感应定律告诉我们:感应电流的磁场总是阻碍引起感应电流的磁通量的变化 |
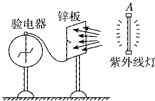 如图所示,一验电器与锌板相连,在A处用一紫外线灯照射锌板,关灯后,指针保持一定偏角.此时锌板带正电.(填“正”或“负”).使验电器指针回到零,再用相同强度的钠灯发出的黄光照射锌板,验电器指针无偏转.那么,若改用强度更大的红外线灯照射锌板,可观察到验电器指针无(填“有”或“无”)偏转.
如图所示,一验电器与锌板相连,在A处用一紫外线灯照射锌板,关灯后,指针保持一定偏角.此时锌板带正电.(填“正”或“负”).使验电器指针回到零,再用相同强度的钠灯发出的黄光照射锌板,验电器指针无偏转.那么,若改用强度更大的红外线灯照射锌板,可观察到验电器指针无(填“有”或“无”)偏转. 如图所示,左端封闭右端开口的细玻璃管水平放置,用h=20cm水银柱封闭了长为L=65cm理想气体,水银柱右端距玻璃管开口端l=10cm.已知外界大气压强p0=76cmHg,温度t=27℃,重力加速度g=9.8m/s2.求:
如图所示,左端封闭右端开口的细玻璃管水平放置,用h=20cm水银柱封闭了长为L=65cm理想气体,水银柱右端距玻璃管开口端l=10cm.已知外界大气压强p0=76cmHg,温度t=27℃,重力加速度g=9.8m/s2.求: 如图所示,单匝线圈在匀强磁场中绕OO′轴从图示位置开始匀速转动,已知从图示位置转动$\frac{π}{6}$时,线圈中感应电动势大小为10V,求:
如图所示,单匝线圈在匀强磁场中绕OO′轴从图示位置开始匀速转动,已知从图示位置转动$\frac{π}{6}$时,线圈中感应电动势大小为10V,求: