题目内容
17. 如图所示,固定在墙角处的木板与水平面的夹角为θ=37°,木板上开有小孔,一根长为1,质量为m的软绳置于木板上,其上端刚好位于小孔处,用细线将质量为m的物块与软绳的上端连接.物块由静止释放后,带动软绳运动,不计所有摩擦.当软绳刚好全部离开木板时(此时物块未到达地面).物块的速度大小为(已知sin37°=0.6,重力加速度大小为g)( )
如图所示,固定在墙角处的木板与水平面的夹角为θ=37°,木板上开有小孔,一根长为1,质量为m的软绳置于木板上,其上端刚好位于小孔处,用细线将质量为m的物块与软绳的上端连接.物块由静止释放后,带动软绳运动,不计所有摩擦.当软绳刚好全部离开木板时(此时物块未到达地面).物块的速度大小为(已知sin37°=0.6,重力加速度大小为g)( )| A. | $\sqrt{gl}$ | B. | $\sqrt{\frac{6}{5}gl}$ | C. | $\sqrt{\frac{13}{10}gl}$ | D. | $\sqrt{2gl}$ |
分析 根据几何关系分别找出物体和软绳重心下落的高度,从而求出两者重力势能的减小量;根据机械能守恒定律即可求得软绳刚好全部离开木板时的速度.
解答 解:在下落过程中,由几何关系可知,重物的重心下降高度为l,软绳重心的下降高度为:
h=0.5l-0.5lsin37°=0.2l
故全过程中重力势能的减小量为:
△EP=mgl+0.2mgl=$\frac{6}{5}$mgl;
根据机械能守恒定律可得:
$\frac{1}{2}$•2mv2=△EP
解得:当软绳刚好全部离开木板时物体的速度为:
v=$\sqrt{\frac{6}{5}gl}$;
故选:B
点评 本题考查机械能守恒定律的应用,注意在分析软绳重力势能的变化时要分析其重心高度的变化,本题也可以设置零势能面,从而确定初末状态的重力势能.

练习册系列答案
相关题目
20.下列说法准确的是( )
| A. | 核反应:${\;}_{92}^{238}U$→${\;}_{90}^{234}Th{+}_{2}^{4}He$属于重核的裂变反应 | |
| B. | 一个氘核(${\;}_{1}^{2}H$)与一个氚核(${\;}_{1}^{3}H$)聚变生成一个氦核(${\;}_{2}^{4}He$)的同时,放出一个中子,其核反应方程是${\;}_{1}^{2}H{+}_{1}^{3}H$→${\;}_{2}^{4}{H}_{e}{+}_{0}^{1}n$ | |
| C. | 质子、中子、α粒子的质量分别是m1、m2、m3,质子和中子结合成一个α粒子,若其核反应方程是${2}_{1}^{1}H{+2}_{0}^{1}n$→${\;}_{2}^{4}{H}_{e}$,则释放的能量为[m3-(2m1+2m2)]c2 | |
| D. | 平均结合能越大表示原子核中的核子结合得越牢固 |
1.2015年11月21日,我国成功将“老挝一号”通信卫星发射升空,卫星顺利进入预定轨道.假设“老挝一号”卫星围绕地球做匀速圆周运动.它距地球表面高度为h,运行的周期为T,地球的半径为R,忽略其他天体对“老挝一号”卫星的引力作用,不考虑地球自转的影响.则( )
| A. | “老挝一号”卫星运行时的向心加速度大小为$\frac{4{π}^{2}(R+h)^{3}}{{R}^{2}{T}^{2}}$ | |
| B. | “老挝一号”卫星运行时的线速度大小为$\frac{2π\sqrt{R(R+h)^{3}}}{RT}$ | |
| C. | 地球表面的重力加速度大小为$\frac{4{π}^{2}(R+h)}{{T}^{2}}$ | |
| D. | 地球的第一宇宙速度大小为$\frac{2π\sqrt{R(R+h)^{3}}}{RT}$ |
6.物理学的发展不是一帆风顺的,经历了反复的争辩,反复的实验,反复的推理等系列过程,伽利略和亚里士多德就是一对有名的“冤家”,亚里士多德结合生活现象,提出“重的物体下落的快,轻的物体下落的慢”的观点时,伽利略进行了智慧型的反驳,提出了“把轻重不同的两个物体连在一起下落,与单独一个物体下落比较,是快了还是慢了”的问题,使亚里士多德张口结舌,下列说法中正确的是( )
| A. | 自由落体运动的快慢与物体的质量有关 | |
| B. | 亚里士多德总是提出错误的观点,阻碍物理学的发展,对物理学的发展没有任何贡献 | |
| C. | 伽利略采用“归谬法”否定了亚里士多德的观点 | |
| D. | 伽利略处于对亚里士多德的偏见,总是无理反驳亚里士多德的观点,事实上,亚里士多德的观点是正确的,铅球和鸡毛从同一高度同时下落,总是铅球先着地 |
 一个质量为m=4kg的物体静止在足够大的水平地面上,物体与地面间的动摩擦因数μ=0.1.从t=0开始,物体受到一个大小和方向呈周期性变化的水平力F作用,力F随时间的变化规律如图所示.求第81s内物体的位移大小和力F对物体所做的功.(g取10m/s2)
一个质量为m=4kg的物体静止在足够大的水平地面上,物体与地面间的动摩擦因数μ=0.1.从t=0开始,物体受到一个大小和方向呈周期性变化的水平力F作用,力F随时间的变化规律如图所示.求第81s内物体的位移大小和力F对物体所做的功.(g取10m/s2) 如图所示,半径未知的1/4光滑圆弧AB与倾角为30°的斜面在B点连接,B点的切线水平,斜面BC长为L,整个装置位于同一竖直面内.现让一个质量为m的小球从圆弧的端点A由静止释放,小球通过B点后恰好落在斜面底端C点处.不计空气阻力.
如图所示,半径未知的1/4光滑圆弧AB与倾角为30°的斜面在B点连接,B点的切线水平,斜面BC长为L,整个装置位于同一竖直面内.现让一个质量为m的小球从圆弧的端点A由静止释放,小球通过B点后恰好落在斜面底端C点处.不计空气阻力.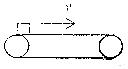 水平方向的传送带以2m/s的速度匀速运动,把一质量为2kg的小物体轻轻放在传送带上左端,经过4s物体到达传送带的右端,已知物体与传送带间的动摩擦因数为0.2,取g=10m/s2.求:
水平方向的传送带以2m/s的速度匀速运动,把一质量为2kg的小物体轻轻放在传送带上左端,经过4s物体到达传送带的右端,已知物体与传送带间的动摩擦因数为0.2,取g=10m/s2.求: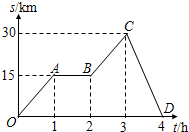 如图所示,是一辆汽车做直线运动的s-t图象,OA段表示汽车做匀速运动(填“匀速”或“变速”);AB段表示汽车处于静止状态(填“静止”或“运动”);0~1h内,汽车的位移大小是15km.
如图所示,是一辆汽车做直线运动的s-t图象,OA段表示汽车做匀速运动(填“匀速”或“变速”);AB段表示汽车处于静止状态(填“静止”或“运动”);0~1h内,汽车的位移大小是15km.