题目内容
20.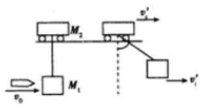 质量为M=18kg的小车放在光滑轨道上,小车下用一根长L=1m的轻绳系一质量M1=1.99kg的木块,一质量m=0.01kg的子弹,以速度v0水平射入木块并留在其中,之后测得木块能摆起的最大摆角θ=60°,求子弹的速度v0(g取10m/s2)
质量为M=18kg的小车放在光滑轨道上,小车下用一根长L=1m的轻绳系一质量M1=1.99kg的木块,一质量m=0.01kg的子弹,以速度v0水平射入木块并留在其中,之后测得木块能摆起的最大摆角θ=60°,求子弹的速度v0(g取10m/s2)
分析 对子弹、小车及木块整体分析,由动量守恒定律可得出动量表达式;在摆动过程机械能守恒,根据机械能守恒列式,联立求解即可.
解答 解:以子弹的方向为正方向;
子弹打M1瞬间,m和M1水平方向动量守恒,而打后M1摆动过程中,m、M1和M2水平方向动量守恒,机械能守恒
子弹打M1时有:mv0=(M1+m)v1
从射入到木块摆至最高点过程中,有:(M1+m)v1=(M1+M2+m)v0′
摆动过程中,对系统机械能守恒:$\frac{1}{2}$(M1+m)v12-$\frac{1}{2}$(M1+M2+m)vt′2=(M1+m)gL(1-cos60°)
由以上几式可得v0=666.7 m/s
答:子弹的速度为666.7m/s.
点评 本题考查动量守恒及机械能守恒定律,要注意明确子弹打入木块后一起摆动过程,机械能才是守恒的.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
10.如图,一带电粒子静止于平行板电容器中,现粒子开始向上运动,其原因可能是( )


| A. | R1 增加 | B. | R2减小 | C. | R3增加 | D. | R3减小 |
8.体重计上站着一个质量为50kg的人,同时放着一个质量为3kg的物体,当此人用20N的竖直向上提这个物体时(g取10m/s2)( )
| A. | 体重计的示数减少2kg | B. | 体重计的示数不会改变 | ||
| C. | 物体受到的合力为10N | D. | 人对磅秤的压力是520N |
15. 如图所示,一物块位于粗糙水平桌面上,现用一大小为F的水平力去推它,使它以加速度a向右运动,若保持力的方向不变而使力增大为2F时,物体的加速度大小( )
如图所示,一物块位于粗糙水平桌面上,现用一大小为F的水平力去推它,使它以加速度a向右运动,若保持力的方向不变而使力增大为2F时,物体的加速度大小( )
 如图所示,一物块位于粗糙水平桌面上,现用一大小为F的水平力去推它,使它以加速度a向右运动,若保持力的方向不变而使力增大为2F时,物体的加速度大小( )
如图所示,一物块位于粗糙水平桌面上,现用一大小为F的水平力去推它,使它以加速度a向右运动,若保持力的方向不变而使力增大为2F时,物体的加速度大小( )| A. | 等于2a | B. | 仍为a | C. | 介于a与2a之间 | D. | 大于2a |
3. 如图所示是做直线运动的甲、乙两位物体相对于同一参数系的位移-时间(x-t)图象,下列说法正确的是( )
如图所示是做直线运动的甲、乙两位物体相对于同一参数系的位移-时间(x-t)图象,下列说法正确的是( )
 如图所示是做直线运动的甲、乙两位物体相对于同一参数系的位移-时间(x-t)图象,下列说法正确的是( )
如图所示是做直线运动的甲、乙两位物体相对于同一参数系的位移-时间(x-t)图象,下列说法正确的是( )| A. | 甲开始启动的时刻比乙早t1 | B. | 当t=t2时,两物体相遇 | ||
| C. | 当t=t2时,两物体相距最远 | D. | 当t=t3时,两物体相距x1 |
7. 两平行金属板水平放置,两板间电压随时间变化关系如图所示,开始上板带正电,若在0~0.1s时间内,质量为m,带负电量为q的粒子在电场中央静止,两板间距离足够大,0.1s时刻开始运动(不计粒子重力).则以下说法正确的是( )
两平行金属板水平放置,两板间电压随时间变化关系如图所示,开始上板带正电,若在0~0.1s时间内,质量为m,带负电量为q的粒子在电场中央静止,两板间距离足够大,0.1s时刻开始运动(不计粒子重力).则以下说法正确的是( )
 两平行金属板水平放置,两板间电压随时间变化关系如图所示,开始上板带正电,若在0~0.1s时间内,质量为m,带负电量为q的粒子在电场中央静止,两板间距离足够大,0.1s时刻开始运动(不计粒子重力).则以下说法正确的是( )
两平行金属板水平放置,两板间电压随时间变化关系如图所示,开始上板带正电,若在0~0.1s时间内,质量为m,带负电量为q的粒子在电场中央静止,两板间距离足够大,0.1s时刻开始运动(不计粒子重力).则以下说法正确的是( )| A. | 粒子先向上运动,后向下运动,t=0.4s时刻在出发点上方 | |
| B. | 粒子先向上运动,后向下运动,t=0.4s时刻在出发点下方 | |
| C. | 粒子在t=0.2s时刻和t=0.3s时刻在同一位置 | |
| D. | 粒子在t=0.3s时刻和t=0.4s时刻速度大小相等,方向相反 |
8. 如图所示,匀强电场中有a、b、c三点,在以它们为顶点的三角形中,∠a=30°,∠c=90°.电场方向与三角形所在平面平行.已知a、b和c点的电势分别为(2-$\sqrt{3}$) V、(2+$\sqrt{3}$) V和2V.该三角形的外接圆上最低、最高电势分别为( )
如图所示,匀强电场中有a、b、c三点,在以它们为顶点的三角形中,∠a=30°,∠c=90°.电场方向与三角形所在平面平行.已知a、b和c点的电势分别为(2-$\sqrt{3}$) V、(2+$\sqrt{3}$) V和2V.该三角形的外接圆上最低、最高电势分别为( )
 如图所示,匀强电场中有a、b、c三点,在以它们为顶点的三角形中,∠a=30°,∠c=90°.电场方向与三角形所在平面平行.已知a、b和c点的电势分别为(2-$\sqrt{3}$) V、(2+$\sqrt{3}$) V和2V.该三角形的外接圆上最低、最高电势分别为( )
如图所示,匀强电场中有a、b、c三点,在以它们为顶点的三角形中,∠a=30°,∠c=90°.电场方向与三角形所在平面平行.已知a、b和c点的电势分别为(2-$\sqrt{3}$) V、(2+$\sqrt{3}$) V和2V.该三角形的外接圆上最低、最高电势分别为( )| A. | (2-$\sqrt{3}$) V、(2+$\sqrt{3}$) V | B. | 0、4 V | C. | (2-$\frac{4\sqrt{3}}{3}$) V、(2+$\frac{4\sqrt{3}}{3}$) V | D. | 0、2$\sqrt{3}$ V |