题目内容
12. 如图所示为宇宙中一恒星系的示意图,A为该星系的一颗行星,它绕中央恒星O的运行轨道近似为圆.已知引力常量为G,天文学家观测得到A行星的运行轨道半径为R0,周期为T0.A行星的半径为r0,其表面的重力加速度为g,不考虑行星的自转.
如图所示为宇宙中一恒星系的示意图,A为该星系的一颗行星,它绕中央恒星O的运行轨道近似为圆.已知引力常量为G,天文学家观测得到A行星的运行轨道半径为R0,周期为T0.A行星的半径为r0,其表面的重力加速度为g,不考虑行星的自转.(1)中央恒星O的质量为多大?
(2)经长期观测发现,A行星实际运动的轨道与圆轨道总存在一些偏离,且周期性地每隔时间t0发生一次最大的偏离.天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知的行星B(假设其运行轨道与A在同一水平面内,且与A的绕行方向相同),它对A行星的万有引力引起A轨道的偏离.(由于B对A的吸引而使A的周期引起的变化可以忽略)根据上述现象及假设,试求未知行星B的运动周期T及轨道半径R.
分析 (1)研究行星绕恒星做匀速圆周运动,根据万有引力提供向心力,列出等式带有周期表达式,再根据已知量解出恒星质量;
(2)先根据多转动一圈时间为t0,求出卫星的周期;然后再根据开普勒第三定律解得轨道半径.
解答 解:(1)设中央恒星质量为M,A行星质量为m,万有引力提供向心力,由牛顿第二定律得:
G$\frac{Mm}{{R}_{0}^{2}}$=m$(\frac{2π}{{T}_{0}})^{2}$R0,解得:M=$\frac{4{π}^{2}{R}_{0}^{3}}{G{T}_{0}^{2}}$;
(2)每隔时间t0发生一次最大的偏离,说明A、B每隔时间t0有一次相距最近的情况,
这时它们转过的角度相差1周(2π),所以有:($\frac{2π}{{T}_{0}}$-$\frac{2π}{T}$)t0=2π,
解得:T=$\frac{{T}_{0}{t}_{0}}{{t}_{0}-{T}_{0}}$,
由开普勒第三定律得:$\frac{{R}^{3}}{{T}^{2}}$=$\frac{{R}_{0}^{3}}{{T}_{0}^{2}}$,
解得:R=$(\frac{{t}_{0}}{{t}_{0}-{T}_{0}})^{\frac{2}{3}}$R0;
答:(1)中央恒星O的质量为:$\frac{4{π}^{2}{R}_{0}^{3}}{G{T}_{0}^{2}}$;
(2)未知行星B的运动周期T为:$\frac{{T}_{0}{t}_{0}}{{t}_{0}-{T}_{0}}$,行星的轨道半径R为:$(\frac{{t}_{0}}{{t}_{0}-{T}_{0}})^{\frac{2}{3}}$R0.
点评 本题考查了万有引力定律的应用,考查了求质量、周期与轨道半径问题,知道万有引力提供向心力是解题的关键,应用万有引力公式与牛顿第二定律可以解题;从本题可以看出,通过测量环绕天体的轨道半径和公转周期,可以求出中心天体的质量.

| A. | 电荷量 | B. | 电场力 | C. | 电势 | D. | 电势能 |
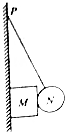 如图所示,光滑小球N用轻绳系在竖直墙壁上的P点,在球N和墙壁之间夹有一长方体物块M,系统处于静止状态.现用拇指将绳按在墙上从P点沿墙缓慢下移少许,则在缓慢下移过程中( )
如图所示,光滑小球N用轻绳系在竖直墙壁上的P点,在球N和墙壁之间夹有一长方体物块M,系统处于静止状态.现用拇指将绳按在墙上从P点沿墙缓慢下移少许,则在缓慢下移过程中( )| A. | 细绳对球N的拉力逐渐变大 | B. | 物块M受到墙壁的弹力逐渐增大 | ||
| C. | 物块M受到墙壁的摩擦力大小不变 | D. | 物块M可能沿墙下滑 |
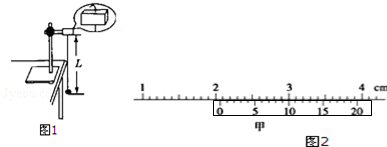
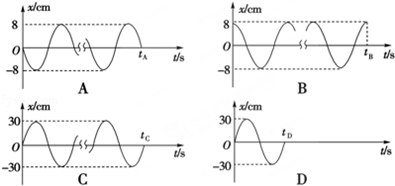
 一宇航员到达半径为R、密度均匀的某星球表面,做如下实验:用不可伸长的轻绳拴一质量为m的小球,上端固定在O点,如图1所示,在最低点给小球某一初速度,使其绕O点的竖直面内做圆周运动,测得绳的拉力F大小随时间t的变化规律如图2所示.F1=7F2.设R、m、引力常量G以及F1为已知量,忽略各种阻力说法正确的是( )
一宇航员到达半径为R、密度均匀的某星球表面,做如下实验:用不可伸长的轻绳拴一质量为m的小球,上端固定在O点,如图1所示,在最低点给小球某一初速度,使其绕O点的竖直面内做圆周运动,测得绳的拉力F大小随时间t的变化规律如图2所示.F1=7F2.设R、m、引力常量G以及F1为已知量,忽略各种阻力说法正确的是( )| A. | 该星球表面的重力加速度为$\frac{{F}_{1}}{7m}$ | |
| B. | 卫星绕该星球的第一宇宙速度为$\sqrt{\frac{Gm}{R}}$ | |
| C. | 该星球的质量为$\frac{{F}_{1}{R}^{2}}{7Gm}$ | |
| D. | 小球在圆周运动过程中,加速度方向始终指向圆心,角速度大小不断变化 |
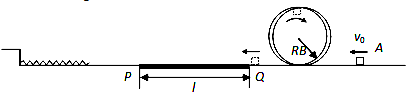
 如图所示,某人站在距水平地面高h处的山顶用球拍水平击出一个质量为m的小球(不计空气阻力),球刚好落在图中L处的A点,则下列说法正确的是( )
如图所示,某人站在距水平地面高h处的山顶用球拍水平击出一个质量为m的小球(不计空气阻力),球刚好落在图中L处的A点,则下列说法正确的是( )| A. | 球被击出后在水平方向做匀加速直线运动 | |
| B. | 该球从被击出到落至A点所用的时间仅由L决足 | |
| C. | 球被击出时的初速度大小为L$\sqrt{\frac{2h}{g}}$ | |
| D. | 击球时球拍对球做的功为$\frac{mg{L}^{2}}{4h}$ |
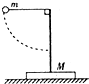 如图所示,放置在水平地面上的支架质量为M,支架顶端用细线拴着的摆球质量为m,现将摆球拉至水平位置,然后从静止释放,摆球运动过程中,支架始终不动,以下说法正确的是( )
如图所示,放置在水平地面上的支架质量为M,支架顶端用细线拴着的摆球质量为m,现将摆球拉至水平位置,然后从静止释放,摆球运动过程中,支架始终不动,以下说法正确的是( )| A. | 在释放瞬间,支架对地面压力为Mg | |
| B. | 在释放瞬间,支架对地面压力为(m+M)g | |
| C. | 摆球到达最低点时,支架对地面压力为(m+M)g | |
| D. | 若在初始位置给物体一向下的初速度,使之恰好能在竖直平面内做圆周运动,则小球在最高点时,支架对地面的压力为Mg |