题目内容
2.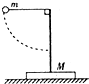 如图所示,放置在水平地面上的支架质量为M,支架顶端用细线拴着的摆球质量为m,现将摆球拉至水平位置,然后从静止释放,摆球运动过程中,支架始终不动,以下说法正确的是( )
如图所示,放置在水平地面上的支架质量为M,支架顶端用细线拴着的摆球质量为m,现将摆球拉至水平位置,然后从静止释放,摆球运动过程中,支架始终不动,以下说法正确的是( )| A. | 在释放瞬间,支架对地面压力为Mg | |
| B. | 在释放瞬间,支架对地面压力为(m+M)g | |
| C. | 摆球到达最低点时,支架对地面压力为(m+M)g | |
| D. | 若在初始位置给物体一向下的初速度,使之恰好能在竖直平面内做圆周运动,则小球在最高点时,支架对地面的压力为Mg |
分析 摆球运动过程中,支架始终不动,在释放摆球的瞬间,分析支架竖直方向受力情况,由平衡条件求解地面对支架的支持力,再由牛顿第三定律得到支架对地面的压力.摆球从释放到到达最低点时,机械能守恒,由机械能守恒定律和牛顿第二定律求出摆球到达最低点时细线的拉力,再求解支架对地面的压力.小球恰好在竖直平面内做圆周运动时,在最高点时绳子拉力为零.
解答 解:AB、在释放摆球的瞬间,支架竖直方向受到重力Mg和地面的支持力N1,由平衡条件知,N1=Mg,根据牛顿第三定律得知,支架对地面的压力N1′=N1=Mg.故A正确.
C、设摆球到达最低点时速度大小为v,摆长为L,由机械能守恒定律得:
mgL=$\frac{1}{2}m{v}^{2}$…①
摆球到达最低点时,由牛顿第二定律有:F-mg=m$\frac{{v}^{2}}{L}$…②
联立①②得细线对球的拉力:F=3mg
结合牛顿第三定律,得球对细线的拉力大小 F′=3mg,方向竖直向下
则支架对地面的压力大小为:N2=Mg+F′=(3m+M)g.故C错误.
D、小球恰好在竖直平面内做圆周运动时,在最高点时绳子拉力为零,则小球在最高点时,支架对地面的压力为Mg,故D正确.
故选:AD
点评 本题考查平衡条件、机械能守恒定律和牛顿运动定律,要知道摆球到达最低点时细线的拉力等于3mg,与摆长无关,这是经常用到的结论,最好记住.

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
10.随着“神州九号”与“天宫一号”成功牵手,我国将于2020年前发射月球登陆器.月球登陆器返回时,先由月球表面发射后绕月球在近月圆轨道上飞行,经轨道调整后与在较高圆轨道上运行的轨道舱对接,对接完成后再经加速脱离月球飞回地球.下列关于此过程的描述,正确的是( )
| A. | 登陆器在近月圆轨道上运行的速度必须大于月球第一宇宙速度 | |
| B. | 登陆器在近月圆轨道上必须加速才能与轨道舱对接 | |
| C. | 登录器与轨道舱对接后的运动周期小于对接前登录器的运动周期 | |
| D. | 登录器在近月圆轨道上飞行的速度大于轨道舱的运行速度 |
17.若认为行星绕太阳做圆周运动,则太阳对行星的引力( )
| A. | 提供行星运动的向心力 | B. | 与行星质量无关 | ||
| C. | 与行星和太阳的质量之和成正比 | D. | 与行星和太阳间的距离成反比 |
14. 在探究磁场产生电流的条件,做了下面实验:
在探究磁场产生电流的条件,做了下面实验:
请填写观察到现象
 在探究磁场产生电流的条件,做了下面实验:
在探究磁场产生电流的条件,做了下面实验:请填写观察到现象
| 实验操作 | 电流表的指针(偏转或不偏转) |
| 1、接通开关瞬间 | 偏转 |
| 2、接通开关,变阻器滑片移动 | 偏转 |
| 3、接通开关,变阻器滑片不移动 | 不偏转 |
 如图所示为宇宙中一恒星系的示意图,A为该星系的一颗行星,它绕中央恒星O的运行轨道近似为圆.已知引力常量为G,天文学家观测得到A行星的运行轨道半径为R0,周期为T0.A行星的半径为r0,其表面的重力加速度为g,不考虑行星的自转.
如图所示为宇宙中一恒星系的示意图,A为该星系的一颗行星,它绕中央恒星O的运行轨道近似为圆.已知引力常量为G,天文学家观测得到A行星的运行轨道半径为R0,周期为T0.A行星的半径为r0,其表面的重力加速度为g,不考虑行星的自转. 如图所示,小明同学将一小球沿桌面水平抛出,已知小球落地时的速度方向与水平方向的夹角为θ.若不计空气阻力,取地面为重力势能参考平面,求小球被抛出时的动能与重力势能之比等于多少?
如图所示,小明同学将一小球沿桌面水平抛出,已知小球落地时的速度方向与水平方向的夹角为θ.若不计空气阻力,取地面为重力势能参考平面,求小球被抛出时的动能与重力势能之比等于多少?
 ”表示)(请画在图2方框内);
”表示)(请画在图2方框内); 有两根光滑绝缘杆,它们可在同一竖直平面内绕O点无摩擦转动.两杆上各穿有质量为m,带电量分别为q1、q2的小球.两杆与水平面间夹角相等都为θ时,两小球在同一水平面上且处于平衡状态时,它们到O点距离均为l.θ取何值时小球到O点的距离l最小?( )
有两根光滑绝缘杆,它们可在同一竖直平面内绕O点无摩擦转动.两杆上各穿有质量为m,带电量分别为q1、q2的小球.两杆与水平面间夹角相等都为θ时,两小球在同一水平面上且处于平衡状态时,它们到O点距离均为l.θ取何值时小球到O点的距离l最小?( )