题目内容
如图中滑块和小球的质量均为m,滑块可在水平放置的光滑固定导轨上自由滑动,小球与滑块上的悬点O由一不可伸长的轻绳相连,轻绳长为l.开始时,轻绳处于水平拉直状态,小球和滑块均静止.现将小球由静止释放,当小球到达最低点时,滑块刚好被一表面涂有粘性物质的固定挡板粘住,在极短的时间内速度减为零,小球继续向左摆动,当轻绳与竖直方向的夹角θ=60°时小球达到最高点.求:
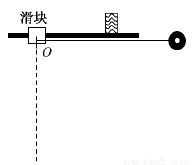
(1)从滑块与挡板接触到速度刚好变为零的过程中,挡板阻力对滑块的冲量;
(2)小球从释放到第一次到达最低点的过程中,绳的拉力对小球做的功的大小.
【答案】
(1)
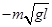(2)
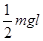
【解析】(1)设小球第一次到达最低点时,滑块和小球速度的大小分别为v1､v2,对于滑块与小球组成的系统,
由机械能守恒定律得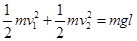
小球由最低点向左摆动到最高点过程,由机械能守恒定律得
联立两式解得
设所求挡板阻力对滑块的冲量为I,规定动量方向向右为正,对滑块由动量定理得I=0-mv1
解得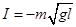
(2)小球从开始释放到第一次到达最低点的过程中,设绳的拉力对小球做功为W,由动能定理得
将v2代入解得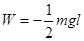
小球从释放到第一次到达最低点的过程中,绳的拉力对小球做功的大小为
练习册系列答案
阅读快车系列答案
相关题目
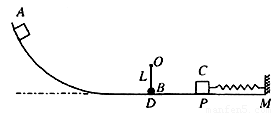
如图所示，竖直放置的圆弧轨道和水平轨道两部分相连． 水平轨道的右侧有一质量为 2m 的滑块C 与轻质弹簧的一端相连，弹簧的另一端固定在竖直的墙M上，弹簧处于原长时，滑块C静止在P 点处；在水平轨道上方O 处，用长为L 的细线悬挂一质量为 m 的小球B，B 球恰好与水平轨道相切，并可绕O点在竖直平面内摆动．质量为 m 的滑块A 由圆弧轨道上静止释放，进入水平轨道与小球B发生弹性碰撞． P 点左方的轨道光滑、右方粗糙，滑块A、C 与PM 段的动摩擦因数均为μ=0.5，A、B、C 均可视为质点，重力加速度为g．
（2008?广州模拟）如图所示的轨道由位于竖直平面的圆弧轨道和水平轨道两部分相连而成．水平轨道的右侧有一质量为2m的滑块C与轻质弹簧的一端相连，弹簧的另一端固定在竖直的墙M上，弹簧处于原长时，滑块C在P点处；在水平轨道上方O处，用长为L的细线悬挂一质量为m的小球B，B球恰好与水平轨道相切于D点，并可绕D点在竖直平面内摆动．质量为m的滑块A由圆弧轨道上静止释放，进入水平轨道与小球B发生碰撞，A、B碰撞前后速度发生交换．P点左方的轨道光滑、右方粗糙，滑块A、C与PM段的动摩擦因数均为μ=
kg的小球A，另一端挂在光滑水平轴O 上，O到小球的距离为L=0.1m，小球跟水平面接触，但无相互作用，在球的两侧等距离处分别固定一个光滑的斜面和一个挡板，如图所示，水平距离s=2m，动摩擦因数μ=0.25．现有一小滑块B，质量也为
，从斜面上滑下，每次与小球碰撞时相互交换速度，且与挡板碰撞不损失机械能．若不计空气阻力，并将滑块和小球都视为质点，g取10m/s2，（斜面底端与水平面光滑连接，即滑块通过连接点时无机械能损失）。试问：
处滑下与小球第一次碰撞后，使小球恰好在竖直平面内做完整的圆周运动，求此高度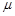
=0.5，A、B、C 均可视为质点，重力加速度为g．
L，求弹簧的最大弹性势能。