题目内容
15.一物体静止在斜面底端,在沿斜面的拉力作用下沿斜面向上加速运动,加速度大小为a,经过时间t秒撤去拉力,物体又经过t秒恰好回到斜面底端,求物体沿斜面向上运动的最大距离.分析 根据两段过程中的时间关系,位移关系,结合速度公式和位移公式求出加速度大小的关系,结合速度位移公式求出物体沿斜面减速上滑的距离,结合匀加速直线运动的位移求出物体沿斜面向上运动的最大距离.
解答 解:拉力作用在物体上,根据运动学公式有:
v=at,
${x}_{1}=\frac{1}{2}a{t}^{2}$,
撤去拉力后,根据运动学公式有:$-{x}_{1}=vt-\frac{1}{2}a′{t}^{2}$,
联立解得a′=3a,
撤去拉力后,物体沿斜面减速到零时上滑的距离为x2,根据运动学公式有:
0-v2=2(-a′)x2,
物体沿斜面上海的最大距离为x=x1+x2,
联立解得x=$\frac{2}{3}a{t}^{2}$.
答:物体沿斜面向上运动的最大距离为$\frac{2}{3}a{t}^{2}$.
点评 本题考查了运动学公式的基本运用,知道撤去拉力过程中,物体的速度虽然会反向,但是加速度不变,可以全过程运用运动学公式进行求解.

练习册系列答案
相关题目
6.下列的说法中正确的是( )
| A. | 只有很小的物体才能看作质点 | |
| B. | 说“月亮在乌云中穿行”是以月亮为参考系的 | |
| C. | 研究地球绕太阳的运动时,可把地球看作质点 | |
| D. | 研究一辆火车通过一站牌的时间,可以将货车看作质点 |
3.同一平面内几组共点力中,它们的合力可能使物体处于平衡状态的有( )
| A. | 5N、9N、15N | B. | 9N、12N、20N | C. | 5N、12N、6N | D. | 10N、14N、24N |
10.如图所示,是甲、乙两物体做直线运动的位移-时间图象,则下列说法正确的是( )


| A. | 甲乙两物体同时出发 | B. | 当t=t2时,两物体速度相等 | ||
| C. | 乙物体的速度比甲物体的速度大 | D. | 甲、乙两物体运动方向相同 |
7.在较暗的房间里,从射进来的阳光中,可以看到悬浮在空气中的微粒在不停地运动,这些微粒的运动( )
| A. | 是空气分子对微粒的不平衡性撞击引起的布朗运动 | |
| B. | 是空气对流和重力引起的运动 | |
| C. | 是微粒在重力作用下的自由落体运动 | |
| D. | 是由于分子无规则运动引起的扩散现象 |
 用原长为15cm的弹簧竖直吊起一块木块,稳定后弹簧长23cm,用这弹簧在水平桌面上水平匀速拉动该木块,弹簧的长为17cm,求木块与桌面间的动摩擦因数.
用原长为15cm的弹簧竖直吊起一块木块,稳定后弹簧长23cm,用这弹簧在水平桌面上水平匀速拉动该木块,弹簧的长为17cm,求木块与桌面间的动摩擦因数. 在真空中,有速度v=1.4×106m/s的电子束,由A点水平射入磁感应强度B=2×10-4T、宽度d=3.46cm的匀强磁场中,磁场方向垂直纸在向里,如图所示,已知电子质量m=9.1×10-31kg,电量e=1.6×10-19C,求电子束射出磁场时在竖直方向偏移的距离D.
在真空中,有速度v=1.4×106m/s的电子束,由A点水平射入磁感应强度B=2×10-4T、宽度d=3.46cm的匀强磁场中,磁场方向垂直纸在向里,如图所示,已知电子质量m=9.1×10-31kg,电量e=1.6×10-19C,求电子束射出磁场时在竖直方向偏移的距离D.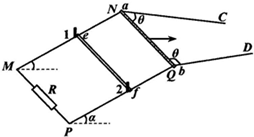 如图所示,金属导轨MNC和PQD,MN与PQ平行且间距为L,所在平面与水平面夹角为α,N、Q连线与MN垂直,M、P间接有阻值为R的电阻;光滑直导轨NC和QD在同一水平面内,与NQ的夹角都为锐角θ.均匀金属棒ab和ef质量均为m,长均为L,ab棒初始位置在水平导轨上与NQ重合;ef棒垂直放在倾斜导轨上,与导轨间的动摩擦因数为μ(μ较小),由导轨上的小立柱1和2阻挡而静止.空间有方向竖直的匀强磁场(图中未画出).两金属棒与导轨保持良好接触.不计所有导轨和ab棒的电阻,ef棒的阻值为R,最大静摩擦力与滑动摩擦力大小相等,忽略感应电流产生的磁场,重力加速度为g.
如图所示,金属导轨MNC和PQD,MN与PQ平行且间距为L,所在平面与水平面夹角为α,N、Q连线与MN垂直,M、P间接有阻值为R的电阻;光滑直导轨NC和QD在同一水平面内,与NQ的夹角都为锐角θ.均匀金属棒ab和ef质量均为m,长均为L,ab棒初始位置在水平导轨上与NQ重合;ef棒垂直放在倾斜导轨上,与导轨间的动摩擦因数为μ(μ较小),由导轨上的小立柱1和2阻挡而静止.空间有方向竖直的匀强磁场(图中未画出).两金属棒与导轨保持良好接触.不计所有导轨和ab棒的电阻,ef棒的阻值为R,最大静摩擦力与滑动摩擦力大小相等,忽略感应电流产生的磁场,重力加速度为g.