题目内容
3. 如图所示,圆柱形区域的半径为R,在区域同有垂直于纸面向里,磁感应强度大小为B的匀强磁场;对称放置的三个相同的电容器.极板间距为d,极板电压为U,与磁场相切的极板,在切点处均有一小孔,一带电粒子,质量为m,带电荷量为+q,自某电容器极板上的M点由静止释放,M点在小孔a的正上方,若经过一段时间后,带电粒子又恰好返回M点,不计带电粒子所受重力.求:
如图所示,圆柱形区域的半径为R,在区域同有垂直于纸面向里,磁感应强度大小为B的匀强磁场;对称放置的三个相同的电容器.极板间距为d,极板电压为U,与磁场相切的极板,在切点处均有一小孔,一带电粒子,质量为m,带电荷量为+q,自某电容器极板上的M点由静止释放,M点在小孔a的正上方,若经过一段时间后,带电粒子又恰好返回M点,不计带电粒子所受重力.求:(1)带电粒子在磁场中运动的轨道半径;
(2)U与B所满足的关系式;
(3)带电粒子由静止释放到再次返回M点所经历的时间.
分析 (1)画出运动的轨迹,根据几何关系求得半径;
(2)根据动能定理求出电子加速后的速度,然后由洛伦兹力提供向心力即可求出磁感应强度;
(3)求出粒子做圆周运动的周期,结合运动的轨迹求出电子在各段上的时间,求和即可.
解答 解:(1)磁场中原半径r圆心角为120°的圆弧与半径R圆心角为60°的轨道圆弧的两段详解在相同的两点,由几何关系解出:r=$\sqrt{3}$R;
(2)设粒子加速后获得的速度为v,进入磁场后做匀速圆周运动的半径为R.
由动能定理得:qU=$\frac{1}{2}$mv2-0,
由洛伦兹力提供向心力,得:qvB=m$\frac{{v}^{2}}{r}$,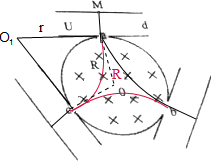
由几何关系得:r=Rtan60°
联立以上公式得:B=$\frac{1}{R}$$\sqrt{\frac{2mU}{3q}}$;
(3)根据运动电荷在磁场中做匀速圆周运动的周期公式T=$\frac{2πm}{qB}$=2πR$\sqrt{\frac{3m}{2qU}}$,
依题意分析可知粒子在磁场中运动一次所经历的时间为$\frac{1}{6}$T,故粒子在磁场中运动的总时间t1=3×$\frac{1}{6}$=πR$\sqrt{\frac{3m}{2qU}}$,
而粒子在匀强电场中做一类 似竖直上抛运动,所经历的时间t2,由s=$\frac{1}{2}$at2可求得:t2=2$\sqrt{\frac{2d}{a}}$.
因为a=$\frac{qU}{md}$,
所以t2=2d$\sqrt{\frac{2m}{qU}}$,粒子在电场中运动的总时间为:6d$\sqrt{\frac{2m}{qU}}$.?
带电粒子由静止释放到再次返回M点所经历的时间为:?
t=t1+3t2=πR$\sqrt{\frac{3m}{2qU}}$+6d$\sqrt{\frac{2m}{qU}}$.?
答:(1)带电粒子在磁场中运动的轨道半径为$\sqrt{3}$R;
(2)U与B所满足的关系式为:B=$\frac{1}{R}$$\sqrt{\frac{2mU}{3q}}$;
(3)带电粒子由静止释放到再次返回M点所经历的时间为πR$\sqrt{\frac{3m}{2qU}}$+6d$\sqrt{\frac{2m}{qU}}$.
点评 带电粒子在电磁场中的运动,要注意灵活选择物理规律,电场中一般由动能定理或类平抛的规律求解,而磁场中粒子做圆周运动,应由向心力公式及几何关系求解.

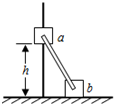 如图所示,滑块a、b的质量均为m,a套在固定光滑竖直杆上,与光滑水平地面相距h,b放在地面上,a、b通过铰链用刚性轻杆连接,不计摩擦,a、b可视为质点,重力加速度大小为g.下列判断正确的是( )
如图所示,滑块a、b的质量均为m,a套在固定光滑竖直杆上,与光滑水平地面相距h,b放在地面上,a、b通过铰链用刚性轻杆连接,不计摩擦,a、b可视为质点,重力加速度大小为g.下列判断正确的是( )| A. | a下落的某段过程中,b对地面的压力可能大于b受到地面的支持力 | |
| B. | a落地前,轻杆对b先做正功后做负功 | |
| C. | a下落的某段过程中,其加速度大小可能大于g | |
| D. | a落地前瞬间a的机械能最小,此时b对地面的压力大小等于mg |
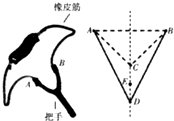 “弹弓”一直是孩子们最喜爱的弹射类玩具之一,其构造如图所示,橡皮筋两端点A、B固定在把手上,橡皮筋ACB恰好处于原长状态,在C处(AB连线的中垂线上)放一固体弹丸,一手执把,另一手将弹丸拉至D点放手,弹丸就会在橡皮筋的作用下迅速发射出去,打击目标,现将弹丸竖直向上发射,已知E是CD中点,则( )
“弹弓”一直是孩子们最喜爱的弹射类玩具之一,其构造如图所示,橡皮筋两端点A、B固定在把手上,橡皮筋ACB恰好处于原长状态,在C处(AB连线的中垂线上)放一固体弹丸,一手执把,另一手将弹丸拉至D点放手,弹丸就会在橡皮筋的作用下迅速发射出去,打击目标,现将弹丸竖直向上发射,已知E是CD中点,则( )| A. | 从D到C,弹丸的机械能守恒 | |
| B. | 从D到C,弹丸的动能一直在增大 | |
| C. | 从D到C,弹丸的机械能先增大后减小 | |
| D. | 从D到E弹丸增加的机械能大于从E到C弹丸增加的机械能 |
 有一质量为m的小木块,由碗边滑向碗底,碗的内表面是半径为R的圆弧,由于摩擦力的作用,木块运动的速率不变,则木块( )
有一质量为m的小木块,由碗边滑向碗底,碗的内表面是半径为R的圆弧,由于摩擦力的作用,木块运动的速率不变,则木块( )| A. | 对碗的压力大小不变 | B. | 对碗的压力始终大于重力 | ||
| C. | 运动的加速度恒定 | D. | 所受合外力大小不变 |
| A. | 电场中某点场强的方向跟电荷在该点受电场力的方向相同 | |
| B. | 电场中某点的场强为E=$\frac{F}{q}$,当检验电荷的电量为2q时,则该点场强为E | |
| C. | 电场中某点的场强为E,若检验电荷从该点移走,则该点电场强度为零 | |
| D. | 电场中某点场强E=$\frac{F}{q}$,若检验电荷为-2q时,则该点场强仍为E |
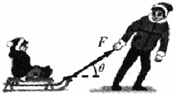 小孩和雪橇的总质量为46kg,在与水平面成37°角的拉力F的作用下,沿水平地面做直线运动,经过0.5s速度由0.3m/s均匀地增加到0.8m/s,已知雪橇与地面的动摩擦因数μ=0.2,求作用力F的大小及地面受到的压力.(取g=10m/s2)
小孩和雪橇的总质量为46kg,在与水平面成37°角的拉力F的作用下,沿水平地面做直线运动,经过0.5s速度由0.3m/s均匀地增加到0.8m/s,已知雪橇与地面的动摩擦因数μ=0.2,求作用力F的大小及地面受到的压力.(取g=10m/s2)