题目内容
12.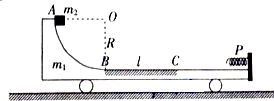 静放在光滑水平面上的小车左端有$\frac{1}{4}$光滑圆弧滑道AB,与水平滑到相切于B点,水平滑道上的BC部分粗糙,其余部分光滑,右端固定一个轻弹簧P,整个滑道质量为m1,如图所示,现让质量为m2的滑块(可视为质点)自A点由静止释放,滑块滑过BC后与小车右端弹簧碰撞,第一次被弹簧弹回后没有再滑上圆弧滑道,已知粗糙水平滑道BC长l=1.0m,滑块与BC间的动摩擦因数μ=0.15,m1=2m2,取g=10m/s2,求:
静放在光滑水平面上的小车左端有$\frac{1}{4}$光滑圆弧滑道AB,与水平滑到相切于B点,水平滑道上的BC部分粗糙,其余部分光滑,右端固定一个轻弹簧P,整个滑道质量为m1,如图所示,现让质量为m2的滑块(可视为质点)自A点由静止释放,滑块滑过BC后与小车右端弹簧碰撞,第一次被弹簧弹回后没有再滑上圆弧滑道,已知粗糙水平滑道BC长l=1.0m,滑块与BC间的动摩擦因数μ=0.15,m1=2m2,取g=10m/s2,求:(1)$\frac{1}{4}$光滑圆弧滑道AB的半径大小范围;
(2)整个过程中小车获得的最大速度.
分析 (1)系统水平方向动量守恒,应用动量守恒定律与能量守恒定律求出R的临界值,然后确定其范围.
(2)分析清楚过程,确定小车受到最大的位置,然后应用动量守恒定律与能量守恒定律求出最大速度.
解答 解:(1)小车与滑块组成的系统在水平方向所受合外力为零,系统在水平方向动量守恒,
系统初状态在水平方向动量为零,由动量守恒定律可知,系统在末状态系统动量为零,
最终小车与滑块均静止,小车与滑块的动能都为零,由能量守恒定律可知,滑块重力势能的减少量转化为内能,
当滑块静止在C处时,圆弧滑道的半径最小,由能量守恒定律得:
m2gR最小=μm2gl,
解得:R最小=0.15m,
当滑块最终静止在B处时,圆弧滑道的半径最大,由能量守恒定律得:
m2gR最大=μm2g•2l,
解得:R最大=0.3m,
则$\frac{1}{4}$光滑圆弧滑道AB的半径大小范围是:0.15m≤R≤0.3m;
(2)当滑块由静止刚滑到圆弧滑道的最低点时,小车的速度最大,小车与滑块组成的系统在水平方向动量守恒,以向右为正方向,由动量守恒定律得:
m2v滑块-m1v小车=0,
由机械能守恒定律得:m2gR=$\frac{1}{2}$m2v滑块2+$\frac{1}{2}$m1v小车2,
已知:m1=2m2,
解得:v小车=$\sqrt{\frac{gR}{3}}$,
由于0.15m≤R≤0.3m,
则:R=0.3m时,小车的速度最大,v小车最大=$\sqrt{\frac{g{R}_{最大}}{3}}$=$\sqrt{\frac{10×0.3}{3}}$=1m/s;
答:(1)$\frac{1}{4}$光滑圆弧滑道AB的半径大小范围是:0.15m≤R≤0.3m;
(2)整个过程中小车获得的最大速度是1m/s.
点评 本题考查了求半径范围、小车的最大速度,分析清楚物体运动过程是正确解题的关键,应用动量守恒定律、能量守恒定律、机械能守恒定律即可正确解题.

| A. | V1是瞬时速度,V2是平均速度 | B. | V1是平均速度,V2是瞬时速度 | ||
| C. | V1,V2都是瞬时速度 | D. | V1,V2都是平均速度 |
 如图所示,在光滑水平面上,有竖直向下的匀强磁场,分布在宽度为L的区域内,两个边长均为a(a<L)的单匝闭合正方形线圈甲和乙,分别用相同材料不同粗细的导线绕制而成,且导线的横截面积S甲:S乙=1:3.将线圈置于光滑水平面上且位于磁场的左边界,并使两线圈获得大小相等、方向水平向右的初速度,若甲线圈刚好能滑离磁场,则( )
如图所示,在光滑水平面上,有竖直向下的匀强磁场,分布在宽度为L的区域内,两个边长均为a(a<L)的单匝闭合正方形线圈甲和乙,分别用相同材料不同粗细的导线绕制而成,且导线的横截面积S甲:S乙=1:3.将线圈置于光滑水平面上且位于磁场的左边界,并使两线圈获得大小相等、方向水平向右的初速度,若甲线圈刚好能滑离磁场,则( )| A. | 乙线圈也刚好能滑离磁场 | |
| B. | 两线圈进入磁场过程中通过导线横截面积电量相同 | |
| C. | 两线圈完全进入磁场后的动能相同 | |
| D. | 甲线圈进入磁场过程中产生热量Q1与乙线圈进入磁场过程中产生热量Q2之比为$\frac{Q_1}{Q_2}=\frac{1}{3}$ |
| A. | 只有磁铁周围才有磁场 | |
| B. | 电流能产生磁场说明电和磁是有联系的 | |
| C. | 电荷的周围一定有电场和磁场 | |
| D. | 永久磁铁的磁场与电流周围的磁场是两种不同的磁场 |
| A. | 当电源的电压加在起辉器两端时,氖气放电发出辉光并产生热量,导致双金属片受热膨胀 | |
| B. | 当电源的电压加在启动器两极后,动、静触片间辉光放电,受热膨胀两触片接触而不分 | |
| C. | 起辉器中U形动触片是由单金属片制成 | |
| D. | 当动、静两触片接触后,氖气停止放电、温度降低,两触片分离 |
 如图所示是测量通电螺线管内部磁感应强度的一种装置:把一个很小的测量线圈放在待测处(测量线圈平面与螺线管轴线垂直),将线圈与可以测量电荷量的冲击电流计G串联,螺线管通过图中虚线框内的双刀双掷开关K与电源组成闭合回路.当将双刀双掷开关K由位置1拨到位置2时,测得通过测量线圈的电荷量为q.已知测量线圈的匝数为N,截面积为S,测量线圈和G串联回路的总电阻为R.下列判断正确的是( )
如图所示是测量通电螺线管内部磁感应强度的一种装置:把一个很小的测量线圈放在待测处(测量线圈平面与螺线管轴线垂直),将线圈与可以测量电荷量的冲击电流计G串联,螺线管通过图中虚线框内的双刀双掷开关K与电源组成闭合回路.当将双刀双掷开关K由位置1拨到位置2时,测得通过测量线圈的电荷量为q.已知测量线圈的匝数为N,截面积为S,测量线圈和G串联回路的总电阻为R.下列判断正确的是( )| A. | 在此过程中,穿过测量线圈的磁通量的变化量△Φ=qR | |
| B. | 在此过程中,穿过测量线圈的磁通量的变化量△Φ=$\frac{qR}{N}$ | |
| C. | 待测处的磁感应强度的大小为B=$\frac{qR}{NS}$ | |
| D. | 待测处的磁感应强度的大小为B=$\frac{qR}{{N}^{2}S}$ |
 矩形线圈abcd,长ab=20cm,宽bc=10cm,匝数n=200,每匝线圈电阻R=0.25Ω,整个线圈平面均有垂直于线框平面的匀强磁场穿过,磁感应强度B随时间的变化规律如图所示,求
矩形线圈abcd,长ab=20cm,宽bc=10cm,匝数n=200,每匝线圈电阻R=0.25Ω,整个线圈平面均有垂直于线框平面的匀强磁场穿过,磁感应强度B随时间的变化规律如图所示,求 如图所示,在一倾斜放置的U形光滑金属导轨上放置一长为L(与导轨间距宽相等),电阻值为R的铜棒ab,U形导轨的电阻不计,导轨平面与水平面的夹角为θ.整个装置放在磁感应强度为B且与金属导轨平面垂直的匀强磁场中.当铜棒ab以速度v匀速下滑时,求
如图所示,在一倾斜放置的U形光滑金属导轨上放置一长为L(与导轨间距宽相等),电阻值为R的铜棒ab,U形导轨的电阻不计,导轨平面与水平面的夹角为θ.整个装置放在磁感应强度为B且与金属导轨平面垂直的匀强磁场中.当铜棒ab以速度v匀速下滑时,求