题目内容
20.作匀加速直线运动的物体,先后经过A、B两点时的速度分别为v和7v,经历的时间为t,则( )| A. | 前半程速度增加3.5v | B. | 前$\frac{t}{2}$时间内通过的位移为$\frac{11vt}{4}$ | ||
| C. | 后$\frac{t}{2}$时间内通过的位移为$\frac{11vt}{4}$ | D. | 后半程速度增加4v |
分析 解决本题需要掌握:匀变速直线运动的时间中点和位移中点的速度公式,明确公式适用条件和物理量意义.然后直接利用公式求解即可
解答 解:AD、根据中间位置速度公式,有:${v}_{\frac{x}{2}}^{\;}=\sqrt{\frac{{v}_{\;}^{2}+(7v)_{\;}^{2}}{2}}=5v$
前半程速度增加量为:
$△{v}_{1}^{\;}=5v-v=4v$
后半程速度增加量为:$△{v}_{2}^{\;}=7v-5v=2v$,故AD错误;
BC、中间时刻的速度为:${v}_{\frac{t}{2}}^{\;}=\frac{v+7v}{2}=4v$
前$\frac{t}{2}$时间平均速度为:$\overline{{v}_{1}^{\;}}=\frac{v+4v}{2}=\frac{5}{2}v$
前$\frac{t}{2}$时间内通过的位移为:${x}_{1}^{\;}=\overline{{v}_{1}^{\;}}•\frac{t}{2}=\frac{5}{2}v•\frac{t}{2}=\frac{5}{4}vt$
后$\frac{t}{2}$时间平均速度为:$\overline{{v}_{2}^{\;}}=\frac{4v+7v}{2}=\frac{11}{2}v$
后$\frac{t}{2}$时间内通过的位移为:${x}_{2}^{\;}=\overline{{v}_{2}^{\;}}•\frac{t}{2}=\frac{11}{2}v•\frac{t}{2}=\frac{11}{4}vt$,故B错误,C正确;
故选:C
点评 本题考查了匀变速直线运动推论公式的应用,对于这些推论公式既要会推导也要明确其适用条件并能灵活应用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.下列关于弹力和摩擦力说法正确的是( )
| A. | 有摩擦力一定用弹力 | B. | 有弹力一定有摩擦力 | ||
| C. | 摩擦力和弹力都是非接触力 | D. | 以上说法均不正确 |
8.下列每组中三个物理量均为矢量的是( )
| A. | 摩擦力、加速度、电场强度 | B. | 动能、势能、电势 | ||
| C. | 功、势能、电流强度 | D. | 质量、时间、位移 |
15. 图中的实线表示电场线,虚线表示只受电场力作用的带电粒子的运动轨迹,粒子先经过M点,再经过N点,可以判定( )
图中的实线表示电场线,虚线表示只受电场力作用的带电粒子的运动轨迹,粒子先经过M点,再经过N点,可以判定( )
 图中的实线表示电场线,虚线表示只受电场力作用的带电粒子的运动轨迹,粒子先经过M点,再经过N点,可以判定( )
图中的实线表示电场线,虚线表示只受电场力作用的带电粒子的运动轨迹,粒子先经过M点,再经过N点,可以判定( )| A. | M点的电势大于N点的电势 | |
| B. | M点的电势小于N点的电势 | |
| C. | 粒子在M点的电势能大于在N点的电势能 | |
| D. | 粒子在M点的电势能小于在N点的电势能 |
5.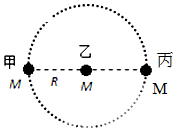 如图所示,甲、乙、丙是位于同一直线上的离其它恒星较远的三颗恒星,甲、丙围绕乙在半径为R的圆轨道上运行,若三颗星质量均为M,万有引力常量为G,则( )
如图所示,甲、乙、丙是位于同一直线上的离其它恒星较远的三颗恒星,甲、丙围绕乙在半径为R的圆轨道上运行,若三颗星质量均为M,万有引力常量为G,则( )
 如图所示,甲、乙、丙是位于同一直线上的离其它恒星较远的三颗恒星,甲、丙围绕乙在半径为R的圆轨道上运行,若三颗星质量均为M,万有引力常量为G,则( )
如图所示,甲、乙、丙是位于同一直线上的离其它恒星较远的三颗恒星,甲、丙围绕乙在半径为R的圆轨道上运行,若三颗星质量均为M,万有引力常量为G,则( )| A. | 甲星所受合力为$\frac{3G{M}^{2}}{4{R}^{2}}$ | |
| B. | 乙星所受合力为$\frac{G{M}^{2}}{{R}^{2}}$ | |
| C. | 甲星做圆周运动的周期为4π$\sqrt{\frac{{R}^{3}}{5GM}}$ | |
| D. | 丙星做圆周运动的线速度大小为5$\sqrt{\frac{GM}{2R}}$ |
9.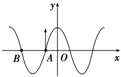 一列简谐横波沿x轴传播,t=0时的波形如图所示,质点A与质点B相距1m,A点速度沿y轴正方向;t=0.02s时,质点A第一次到达正向最大位移处,由此可知( )
一列简谐横波沿x轴传播,t=0时的波形如图所示,质点A与质点B相距1m,A点速度沿y轴正方向;t=0.02s时,质点A第一次到达正向最大位移处,由此可知( )
 一列简谐横波沿x轴传播,t=0时的波形如图所示,质点A与质点B相距1m,A点速度沿y轴正方向;t=0.02s时,质点A第一次到达正向最大位移处,由此可知( )
一列简谐横波沿x轴传播,t=0时的波形如图所示,质点A与质点B相距1m,A点速度沿y轴正方向;t=0.02s时,质点A第一次到达正向最大位移处,由此可知( )| A. | 此波沿x轴负方向传播 | |
| B. | 此波的传播速度为25m/s | |
| C. | 从t=0时起,经过0.04s,质点A沿波传播方向迁移了1m | |
| D. | 能与该波发生干涉的横波的频率一定为25Hz |

 如图所示,一轻质弹簧的劲度系数为500N/m,一端固定于质量为10kg的物体A上,通过该轻质弹簧用一水平力F拉物体(重力加速度g取10m/s2).
如图所示,一轻质弹簧的劲度系数为500N/m,一端固定于质量为10kg的物体A上,通过该轻质弹簧用一水平力F拉物体(重力加速度g取10m/s2). 钍核${\;}_{90}^{230}$Th发生衰变生成镭核${\;}_{88}^{226}$Ra并放出一个粒子.设该粒子的质量为m、电荷量为q,它进入电势差为U的带窄缝的平行平板电极S1和S2间电场时,其速率为v0,经电场加速后,沿Ox方向进入磁感应强度为B、方向垂直纸面向外的有界匀强磁场,Ox垂直平板电极S2,如图所示,整个装置处于真空中.
钍核${\;}_{90}^{230}$Th发生衰变生成镭核${\;}_{88}^{226}$Ra并放出一个粒子.设该粒子的质量为m、电荷量为q,它进入电势差为U的带窄缝的平行平板电极S1和S2间电场时,其速率为v0,经电场加速后,沿Ox方向进入磁感应强度为B、方向垂直纸面向外的有界匀强磁场,Ox垂直平板电极S2,如图所示,整个装置处于真空中.