题目内容
如图所示,用一小段圆弧(其弧长可忽略不计)将水平面AB与倾角为θ=37的斜面平滑相连.一个质量为m=1.0kg的物块(可视为质点)静止在A点.现用水平恒力F=10N作用在物块上,使物块从静止开始做匀加速直线运动,经时间t=1.0s到达B点,此时撤去力F,物块以在B点的速度大小冲上斜面.已知物块与水平地面和斜面间的动摩擦因数均为μ=0.2,重力加速度g取10m/s2,sin37°=0.6,cos37°=0.8.求:(1)物块运动到B点时速度的大小v;
(2)物块在斜面上运动时加速度的大小a;
(3)物块沿斜面向上运动的最大距离s.

【答案】分析:(1)从A到B,根据动量定理列式即可求得速度;
(2)对物体进行受力分析,根据牛顿第二定律列式即可求解加速度;
(3)根据匀变速直线运动位移速度公式即可求解.
解答: 解:(1)从A到B,根据动量定理得:
解:(1)从A到B,根据动量定理得:
(F-μmg)t=mv
解得v=
(2)物块在斜面上受力如图所示:
根据牛顿第二定律得:
mgsinθ+μN=ma
N=mgcosθ
解得:a=7.6m/s2
(3)根据v2=2as
解得:s= =4.2m
=4.2m
答:(1)物块运动到B点时速度的大小为8m/s;
(2)物块在斜面上运动时加速度的大小为7.6m/s2;
(3)物块沿斜面向上运动的最大距离为4.2m.
点评:本题主要考查了动量定理、牛顿第二定律、运动学基本公式的直接应用,难度不大,属于基础题.
(2)对物体进行受力分析,根据牛顿第二定律列式即可求解加速度;
(3)根据匀变速直线运动位移速度公式即可求解.
解答:
 解:(1)从A到B,根据动量定理得:
解:(1)从A到B,根据动量定理得:(F-μmg)t=mv
解得v=

(2)物块在斜面上受力如图所示:
根据牛顿第二定律得:
mgsinθ+μN=ma
N=mgcosθ
解得:a=7.6m/s2
(3)根据v2=2as
解得:s=
 =4.2m
=4.2m答:(1)物块运动到B点时速度的大小为8m/s;
(2)物块在斜面上运动时加速度的大小为7.6m/s2;
(3)物块沿斜面向上运动的最大距离为4.2m.
点评:本题主要考查了动量定理、牛顿第二定律、运动学基本公式的直接应用,难度不大,属于基础题.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 如图所示是某公司设计的“2009”玩具轨道,是用透明的薄壁圆管弯成的竖直轨道,其中引入管道AB及“200”管道是粗糙的,AB是与“2009”管道平滑连接的竖直放置的半径为R=0.4m的
如图所示是某公司设计的“2009”玩具轨道,是用透明的薄壁圆管弯成的竖直轨道,其中引入管道AB及“200”管道是粗糙的,AB是与“2009”管道平滑连接的竖直放置的半径为R=0.4m的 如图所示,虚线所示的圆是某电场中某等势面的截面.a、b两个带电粒子以相同的速度,从电场中 P 点沿等势面的切线方向飞出,粒子仅在电场力作用下的运动轨迹如图中实线所示,则在开始运动的一小段时间内(粒子在图示区域内),下列说法正确的是( )
如图所示,虚线所示的圆是某电场中某等势面的截面.a、b两个带电粒子以相同的速度,从电场中 P 点沿等势面的切线方向飞出,粒子仅在电场力作用下的运动轨迹如图中实线所示,则在开始运动的一小段时间内(粒子在图示区域内),下列说法正确的是( ) (1)某组同学用插针法测平行玻璃砖的折射率,记录下入射、折射、出射光线后,以入射点O为圆心画单位圆,用直尺测得有关线段的长度,如图所示,则下面四个表达式中,正确地表达折射率的关系式是
(1)某组同学用插针法测平行玻璃砖的折射率,记录下入射、折射、出射光线后,以入射点O为圆心画单位圆,用直尺测得有关线段的长度,如图所示,则下面四个表达式中,正确地表达折射率的关系式是 A.将屏移近双缝,干涉条纹间距变窄
A.将屏移近双缝,干涉条纹间距变窄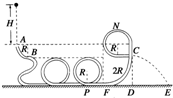 如图所示是某公司设计的“2009”玩具轨道,是用透明的薄壁圆管弯成的竖直轨道,其中引入管道AB及“200”管道是粗糙的,AB是与“2009”管道平滑连接的竖直放置的半径为R=0.4m的
如图所示是某公司设计的“2009”玩具轨道,是用透明的薄壁圆管弯成的竖直轨道,其中引入管道AB及“200”管道是粗糙的,AB是与“2009”管道平滑连接的竖直放置的半径为R=0.4m的