��Ŀ����
5�� ijС������ͼ��ʾ��װ����֤�����غ㶨�ɣ�װ�ù̶���ˮƽ���ϣ�Բ���ι���¶�����ˮƽ������뾶��ͬ��������ˮƽ��Ķ�Ħ��������ͬ��ʵ��ʱ���Ȳ��A��B���������mA��mB������A��δ�Բ���ι����ijһλ���ɾ�ֹ�ͷţ���������ˮƽ���ϻ��о����ƽ��ֵx0��Ȼ�����B�����ڹ���¶�ˮƽ���֣�����A�ӹ����ͬһλ���ɾ�ֹ�ͷţ�����B�������ظ���Σ�
ijС������ͼ��ʾ��װ����֤�����غ㶨�ɣ�װ�ù̶���ˮƽ���ϣ�Բ���ι���¶�����ˮƽ������뾶��ͬ��������ˮƽ��Ķ�Ħ��������ͬ��ʵ��ʱ���Ȳ��A��B���������mA��mB������A��δ�Բ���ι����ijһλ���ɾ�ֹ�ͷţ���������ˮƽ���ϻ��о����ƽ��ֵx0��Ȼ�����B�����ڹ���¶�ˮƽ���֣�����A�ӹ����ͬһλ���ɾ�ֹ�ͷţ�����B�������ظ���Σ���Ϊȷ��ʵ������A�������˶�����mA��mBӦ����Ĺ�ϵ��mA��mB��
��д��ʵ���л���Ҫ�����������������ţ���ײ��A��B����ˮƽ�滬�еľ��룺xA��xB��
������ײǰ�����غ㣬д�������غ�ı���ʽ��mA$\sqrt{{x}_{0}}$=mA$\sqrt{{x}_{A}}$+mB$\sqrt{{x}_{B}}$��
��ȡmA=2mB��x0=1m����A��B��Ϊ��ȫ������ײ����B���еľ���Ϊ$\frac{16}{9}$m��
���� ��Ϊ��ֹ������ײ���������������������Ӧ���ڱ������������
�ڢ�Ӧ�ö����غ㶨���붯�ܶ������ʵ����Ҫ��֤�ı���ʽ��Ȼ��ȷ����Ҫ����������
�ܸ��ݶ����غ㶨�����е���غ㶨�������ײ����ٶȣ�Ȼ�����B���еľ��룮
��� �⣺��Ϊ��ֹ������ײ���������������������Ӧ���ڱ����������������mA��mB��
����ײ�������������˶�������ײ����ٶ�Ϊ��vA��vB��
�ɶ��ܶ����ã�-��mAgx0=0-$\frac{1}{2}$mAv02��v0=$\sqrt{2��g{x}_{0}}$��
-��mAgxA=0-$\frac{1}{2}$mAvA2��vA=$\sqrt{2��g{x}_{A}}$��
-��mBgxB=0-$\frac{1}{2}$mBvB2��vB=$\sqrt{2��g{x}_{B}}$��
�����ײ���̶����غ㣬��mAv0=mAvA+mBvB��
����mA$\sqrt{2��g{x}_{0}}$=mA$\sqrt{2��g{x}_{A}}$+mB$\sqrt{2��g{x}_{B}}$��
�����ã�mA$\sqrt{{x}_{0}}$=mA$\sqrt{{x}_{A}}$+mB$\sqrt{{x}_{B}}$��
ʵ����Ҫ������ײ��A��B����ˮƽ�滬�еľ��룺xA��xB��
���ɢڿ�֪������ײǰ�����غ㣬д�������غ�ı���ʽΪ��
mA$\sqrt{{x}_{0}}$=mA$\sqrt{{x}_{A}}$+mB$\sqrt{{x}_{B}}$��
�������ײ��������ȫ������ײ����ײ����ϵͳ�����غ㣬������Ϊ�������ɶ����غ㶨�ɵã�
mA$\sqrt{{x}_{0}}$=mA$\sqrt{{x}_{A}}$+mB$\sqrt{{x}_{B}}$��
�ɻ�е���غ㶨�ɵã�$\frac{1}{2}$mA��$\sqrt{2��g{x}_{0}}$��2=$\frac{1}{2}$mA��$\sqrt{2��g{x}_{A}}$��2+$\frac{1}{2}$mB��$\sqrt{2��g{x}_{B}}$��2��
��֪��mA=2mB��x0=1m��
��ã�xB=$\frac{16}{9}$m��
�ʴ�Ϊ����mA��mB������ײ��A��B����ˮƽ�滬�еľ��룺xA��xB����mA$\sqrt{{x}_{0}}$=mA$\sqrt{{x}_{A}}$+mB$\sqrt{{x}_{B}}$����$\frac{16}{9}$m��
���� ���⿼�����ж������������ϵ����ʵ����Ҫ����������ʵ����Ҫ��֤����ʽ�����еľ�������⣬ͨ����������ʵ��ԭ���ǽ����ǰ����ؼ���Ӧ�ö����غ㶨�����е���غ㶨�ɿ��Խ��⣮

 ijͬѧ�����г�ʱ�������ǰ�ֵ�Ħ����ΪF1���Ժ��ֵ�Ħ����ΪFf1�������г�ʱ�������ǰ��Ħ����ΪF2���Ժ��ֵ�Ħ����ΪFf2��������
ijͬѧ�����г�ʱ�������ǰ�ֵ�Ħ����ΪF1���Ժ��ֵ�Ħ����ΪFf1�������г�ʱ�������ǰ��Ħ����ΪF2���Ժ��ֵ�Ħ����ΪFf2��������| A�� | F1�복ǰ��������ͬ | B�� | F2�복ǰ��������ͬ | ||
| C�� | Ff1�복ǰ��������ͬ | D�� | Ff2�복ǰ��������ͬ |
| A�� | Һ��û��һ������״���ܹ�������˵��Һ����Ӽ�����������������Ӽ���������һ������Ϊ�� | |
| B�� | ��Һ�������Ӵ�ʱ�γɵ�Һ�屡��и��Ų㣬�ô���Һ�����һ����Һ���ڲ�����ϡ�� | |
| C�� | ��Һ���е糡ǿ�Ȳ�ͬʱ�����Բ�ͬ��ɫ�Ĺ������ǿ�Ȳ�һ��������������ʾ������ɫ����Ҳ��Һ���ʵ���ʾ����ʾ��ɫ��ԭ�� | |
| D�� | ����ѧ���ÿ����е�ˮ������ѹǿ��ͬһ�¶�ʱˮ�ı�����ѹǿ�ı�ֵ��������������ʪ�� | |
| E�� | ֽ�š�����ë������Ʒ��������ˮ����Ϊëϸ�����ԭ�� |
| A�� | �������ݳ�����������Ƶ����������� | |
| B�� | ����������ԭ�Ӻ������к���֮�� | |
| C�� | ԭ�Ӻ�ʽ�ṹģ������¬ɪ���ڦ�����ɢ��ʵ������������ | |
| D�� | ��ԭ���ɽϸ��ܼ�ԾǨ���ϵ��ܼ�ʱ��Ҫ�ͷ�һ��Ƶ�ʵĹ��ӣ�ͬʱ��ԭ�ӵĵ����ܼ�С�����ӵĶ������� | |
| E�� | ������Ԫ�ط�����˥��ʱ���ͷŵĵ�����ԭ�Ӻ��ڵ�����ת��Ϊ����ʱ������ |
| A�� | ���ٶ����� | B�� | ���ڼ�С | C�� | ���ٶȼ�С | D�� | �������� |
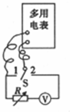 ����ͼʾ��·���Բ������õ���ڵ�صĵ綯��E��ŷķ����100�����ڲ���·���ܵ���r���ṩ�������У����е������ѹ��������3V�����輸ǧŷ���������䣨0��9999.9����������˫������S���������ɣ���Ҫʵ�鲽�����£��벹��������
����ͼʾ��·���Բ������õ���ڵ�صĵ綯��E��ŷķ����100�����ڲ���·���ܵ���r���ṩ�������У����е������ѹ��������3V�����輸ǧŷ���������䣨0��9999.9����������˫������S���������ɣ���Ҫʵ�鲽�����£��벹�������� ��ͼ��ʾ��ֱ�DZ߳�Ϊ0.4m�ĵ���ֱ��б����AOB�̶���ˮƽ�����ϣ�CΪб����е㣮һС���C�����Ϸ���A�ȸߵ�λ������������б����ײ����ƽ���˶���������ײʱ��������ʧ��
��ͼ��ʾ��ֱ�DZ߳�Ϊ0.4m�ĵ���ֱ��б����AOB�̶���ˮƽ�����ϣ�CΪб����е㣮һС���C�����Ϸ���A�ȸߵ�λ������������б����ײ����ƽ���˶���������ײʱ��������ʧ��
