题目内容
4.物体以速度v0水平抛出,若不计空气阻力,则当其竖直分位移与水平位移相等时,以下说法中正确的是( )| A. | 竖直分速度等于水平分速度 | B. | 瞬时速度大小为$\sqrt{2}$v0 | ||
| C. | 运动的时间为$\frac{{2{v_0}}}{g}$ | D. | 运动的位移为$\frac{2v_0^2}{g}$ |
分析 平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据水平位移和竖直位移相等求出运动的时间,结合速度时间公式求出竖直分速度,通过平行四边形定则求出瞬时速度的大小,根据水平位移的大小,结合平行四边形定则求出运动的位移.
解答 解:A、根据${v}_{0}t=\frac{1}{2}g{t}^{2}$得,t=$\frac{2{v}_{0}}{g}$,则竖直分速度vy=gt=2v0,与水平分速度不等,故A错误,C正确.
B、根据平行四边形定则知,瞬时速度的大小v=$\sqrt{{{v}_{0}}^{2}+4{{v}_{0}}^{2}}=\sqrt{5}{v}_{0}$,故B错误.
D、物体的水平位移x=${v}_{0}t=\frac{2{{v}_{0}}^{2}}{g}$,根据平行四边形定则知,运动的位移s=$\sqrt{2}x=\frac{2\sqrt{2}{{v}_{0}}^{2}}{g}$,故D错误.
故选:C.
点评 解决本题的关键知道平抛运动在水平方向和竖直方向上的运动规律,结合运动学公式灵活求解,难度不大.

练习册系列答案
相关题目
15.一定质量的理想气体经过如图所示的变化过程,下列说法正确的是( )
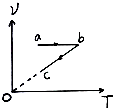

| A. | ab过程中,气体的压强减小 | |
| B. | ab过程中,气体分子的平均动能增大 | |
| C. | bc过程中,气体对外做功,温度降低 | |
| D. | bc过程中,气体的密度增大 |
12. 长度为L=0.50m的轻质细杆OA,A端有一质量为m=3.0kg的小球,如图所示,小球以O点为圆心在竖直平面内做圆周运动,通过最高点时小球的速率是2.0m/s,g取10m/s2,则此时细杆OA受到( )
长度为L=0.50m的轻质细杆OA,A端有一质量为m=3.0kg的小球,如图所示,小球以O点为圆心在竖直平面内做圆周运动,通过最高点时小球的速率是2.0m/s,g取10m/s2,则此时细杆OA受到( )
 长度为L=0.50m的轻质细杆OA,A端有一质量为m=3.0kg的小球,如图所示,小球以O点为圆心在竖直平面内做圆周运动,通过最高点时小球的速率是2.0m/s,g取10m/s2,则此时细杆OA受到( )
长度为L=0.50m的轻质细杆OA,A端有一质量为m=3.0kg的小球,如图所示,小球以O点为圆心在竖直平面内做圆周运动,通过最高点时小球的速率是2.0m/s,g取10m/s2,则此时细杆OA受到( )| A. | 6.0N的拉力 | B. | 6.0N的压力 | C. | 24N的拉力 | D. | 24N的压力 |
19.下列说法正确的是( )
| A. | 液晶的光学性质具有各向异性 | |
| B. | 空气的相对湿度定义为水的饱和蒸汽压与相同温度时空气中所含水蒸气的压强之比 | |
| C. | 小昆虫能在水面上自由走动与表面张力有关 | |
| D. | 玻璃、石墨和金刚石都是晶体,木炭是非晶体 |
9. 如图甲所示,为一列沿x轴传播的简谐横波在t=0时刻的波形图.图乙表示该波传播的介质中x=2m处的质点a从t=0时刻起的振动图象.则下列说法正确的是( )
如图甲所示,为一列沿x轴传播的简谐横波在t=0时刻的波形图.图乙表示该波传播的介质中x=2m处的质点a从t=0时刻起的振动图象.则下列说法正确的是( )
 如图甲所示,为一列沿x轴传播的简谐横波在t=0时刻的波形图.图乙表示该波传播的介质中x=2m处的质点a从t=0时刻起的振动图象.则下列说法正确的是( )
如图甲所示,为一列沿x轴传播的简谐横波在t=0时刻的波形图.图乙表示该波传播的介质中x=2m处的质点a从t=0时刻起的振动图象.则下列说法正确的是( )| A. | t=0时刻,质点a的振动方向为y轴正方向 | |
| B. | 波沿x轴负方向传播 | |
| C. | t=0.25s时,质点a的位移沿y轴正方向 | |
| D. | t=0.25s时,x=4m处的质点b的加速度沿y轴负方向 |
 要测定某电源的电动势和内电阻,以下提供的器材有:
要测定某电源的电动势和内电阻,以下提供的器材有: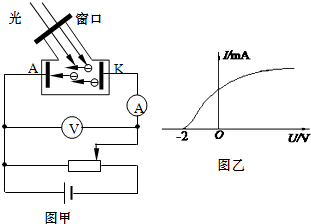
 如图,一上端开口,下端封闭的细长玻璃管,下部有长l1=66cm的水银柱,中间封有长l2=6.5cm的空气柱,上部有长l3=56cm的水银柱,此时水银面恰好与管口平齐.已知大气压强为p0=76cmHg.如果使玻璃管绕底端在竖直平面内缓慢地转动一周,求在开口向下和转回到原来位置时管中空气柱的长度.封入的气体可视为理想气体,在转动过程中没有发生漏气.
如图,一上端开口,下端封闭的细长玻璃管,下部有长l1=66cm的水银柱,中间封有长l2=6.5cm的空气柱,上部有长l3=56cm的水银柱,此时水银面恰好与管口平齐.已知大气压强为p0=76cmHg.如果使玻璃管绕底端在竖直平面内缓慢地转动一周,求在开口向下和转回到原来位置时管中空气柱的长度.封入的气体可视为理想气体,在转动过程中没有发生漏气.