题目内容
如图所示,内壁光滑半径为R的圆形轨道,固定在竖直平面内.质量为m1的小球静止在轨道最低点,另一质量为m2的小球(两小球均可视为质点)从内壁上与圆心O等高的位置由静止释放,运动到最低点时与m1发生碰撞并粘在一起.求:
(1)小球m2刚要与m1发生碰撞时的速度大小;
(2)碰撞后,m1､m2能沿内壁运动所能达到的最大高度(相对碰撞点).
【答案】
(1)
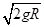(2)
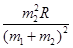
【解析】(1)设小球m2刚要与m1发生碰撞时的速度大小为v0,由机械能守恒定律,得
m2gR=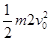
①
解得v0=
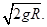②
(2)设两球碰撞后,m1､m2两球粘在一起的速度为v,由动量守恒定律,得
m2v0=(m1+m2)v ③
设两球碰撞后上升的最大高度为h,由机械能守恒守律,得
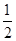(m1+m2)v2=(m1+m2)gh ④
由②③④三式解得h=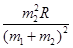 ⑤
练习册系列答案
名校课堂系列答案
相关题目
（2011?商丘二模）如图所示，质量为M、半径为R、内壁光滑的半球形容器静放在粗糙水平地面上，O为球心．有一劲度系数为K的轻弹簧一端固定在半球底部O′处，另一端与质量为m的小球相连，小球静止于P点．已知地面与半球形容器间的动摩擦因数为μ，OP与水平方向的夹角为θ=30°．下列说法正确的是（ ）
如图所示，轻质刚性弹簧两端拴接着可看作质点的小球A和B．当两球静置于内壁光滑半径为R的半球形容器内时，两球之间的距离为
如图所示，光滑内壁的半球形碗，半径为R固定在水平桌面上，质量分别为M、m可视为质点的A、B两球，用轻绳相连（不可伸缩），A由碗沿从静止释放
