题目内容
9. 在“测定匀变速直线运动的加速度”的实验中,打点计时器使用的交流电频率为50Hz,记录小车做匀变速直线运动的纸带如图所示,在纸带上选择清晰的点并标注为0~5六个计数点,相邻两计数点之间还有四个点未画出,纸带旁并排放着带有最小刻度为毫米的刻度尺,其零刻度跟“0”计数点对齐.由图可以读出1、3、5三个计数点跟“0”点的距离d1、d3、d5,完成下列填空:
在“测定匀变速直线运动的加速度”的实验中,打点计时器使用的交流电频率为50Hz,记录小车做匀变速直线运动的纸带如图所示,在纸带上选择清晰的点并标注为0~5六个计数点,相邻两计数点之间还有四个点未画出,纸带旁并排放着带有最小刻度为毫米的刻度尺,其零刻度跟“0”计数点对齐.由图可以读出1、3、5三个计数点跟“0”点的距离d1、d3、d5,完成下列填空:(1)1、3、5三个计数点跟“0”点的距离d1=1.20cm,d2=5.40cm,d3=12.00cm;
(2)通过算可求得小车通过计数点“2”的瞬时速度为0.21m/s;通过计数点“4”的瞬时速度为0.33m/s;
(3)小车的加速度是0.60m/s2.
分析 (1)刻度尺的读数要估读到最小刻度下一位.
(2)匀变速直线运动中某段时间内的平均速度等于中间时刻的瞬时速度,小车通过计数点“2”的瞬时速度等于1、3两点间的平均速度.
(3)求出1、3间的距离和3、5间的距离,根据△x=a(2T)2,求出加速度.
解答 解:(1)按刻度尺的读数规则读数,要估读到最小刻度的下一位,最后一位由于是估读的,d2、d3分别读得5.40cm和12.00cm.
(2)小车通过计数点“2”的瞬时速度可以用“1、3”两计数点间的平均速度来表示,
即v2=$\frac{{d}_{2}-{d}_{1}}{2T}$=$\frac{0.054-0.012}{2×5×0.02}$m/s=0.21m/s;
v4=$\frac{{d}_{3}-{d}_{2}}{2T}$=$\frac{0.12-0.054}{2×5×0.02}$m/s=0.33m/s;
(3)“1、3”:两计数点间距离和“2、4”两计数点间距离分别看成是两段相邻的相等时间(2T)内的位移,由
△x=at2得 a=$\frac{△x}{{t}^{2}}$=$\frac{{(d}_{3}-{d}_{2})-({d}_{2}-{d}_{1})}{4{T}^{2}}$=0.60m/s2
故答案为:(1)1.20,5.40,12.00;(2)0.21,0.33;(3)0.60.
点评 此题重点考查了纸带的处理问题.知道匀变速直线运动中某段时间内的平均速度等于中间时刻的瞬时速度,以及在连续相等时间间隔内的位移差是一恒量,即△x=aT2.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
11.做自由落体运动的小球,通过前一半位移和后一半位移所用时间之比为( )
| A. | 1:2 | B. | $\sqrt{2}$:1 | C. | 1:($\sqrt{2}$+1) | D. | ($\sqrt{2}$+1):1 |
20. 如图所示,质量为m的物体,在与竖直方向成θ角的力F的作用下,从静止开始沿竖直墙壁做匀变速运动.若加速度大小为a,垂直加速度为g,物块与竖直墙壁间的动摩擦因数为μ,则F的大小可能为( )
如图所示,质量为m的物体,在与竖直方向成θ角的力F的作用下,从静止开始沿竖直墙壁做匀变速运动.若加速度大小为a,垂直加速度为g,物块与竖直墙壁间的动摩擦因数为μ,则F的大小可能为( )
 如图所示,质量为m的物体,在与竖直方向成θ角的力F的作用下,从静止开始沿竖直墙壁做匀变速运动.若加速度大小为a,垂直加速度为g,物块与竖直墙壁间的动摩擦因数为μ,则F的大小可能为( )
如图所示,质量为m的物体,在与竖直方向成θ角的力F的作用下,从静止开始沿竖直墙壁做匀变速运动.若加速度大小为a,垂直加速度为g,物块与竖直墙壁间的动摩擦因数为μ,则F的大小可能为( )| A. | $\frac{m(g+a)}{cosθ+μsinθ}$ | B. | $\frac{m(g-a)}{cosθ+μsinθ}$ | C. | $\frac{m(g+a)}{cosθ-μsinθ}$ | D. | $\frac{m(g-a)}{cosθ-μsinθ}$ |
4.-根轻质弹簧一端固定,用大小为F的力压弹簧的另一端,平衡时长度为l1;改用大小为F的力拉弹簧,平衡时长度为l2.弹簧的拉伸或压缩均在弹性限度内,该弹簧的劲度系数为( )
| A. | $\frac{2F}{{l}_{2}-{l}_{1}}$ | B. | $\frac{2F}{{l}_{2}+{l}_{1}}$ | C. | $\frac{F}{{l}_{2}-{l}_{1}}$ | D. | $\frac{F}{{l}_{2}+{l}_{1}}$ |
1. 在如图所示的电路中,灯泡L的电阻大于电源的内阻r,闭合电键S,将滑动变阻器滑片P向左移动一段距离后,下列结论正确的是( )
在如图所示的电路中,灯泡L的电阻大于电源的内阻r,闭合电键S,将滑动变阻器滑片P向左移动一段距离后,下列结论正确的是( )
 在如图所示的电路中,灯泡L的电阻大于电源的内阻r,闭合电键S,将滑动变阻器滑片P向左移动一段距离后,下列结论正确的是( )
在如图所示的电路中,灯泡L的电阻大于电源的内阻r,闭合电键S,将滑动变阻器滑片P向左移动一段距离后,下列结论正确的是( )| A. | 电容器C上电荷量增大 | B. | 电源的输出功率变大 | ||
| C. | 灯泡L变暗 | D. | 电流表读数变小,电压表读数变大 |
18.如图所示是一质点做直线运动的v-t图象,对质点的运动情况下列叙述正确的是( )


| A. | 质点在第2s末改变运动方向 | |
| B. | 质点在前2s内做初速度为零的匀加速运动 | |
| C. | 质点在前2s内位移随时间均匀增加 | |
| D. | 质点在前2s内的位移比后1s内的位移大 |
19.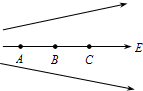 如图所示,实线为电场线,且AB=BC,电场中的A、B、C三点的场强分别为EA、EB、EC,电势分别为φA、φB、φC,AB、BC间的电势差分别为UAB、UBC.下列关系中正确的有( )
如图所示,实线为电场线,且AB=BC,电场中的A、B、C三点的场强分别为EA、EB、EC,电势分别为φA、φB、φC,AB、BC间的电势差分别为UAB、UBC.下列关系中正确的有( )
 如图所示,实线为电场线,且AB=BC,电场中的A、B、C三点的场强分别为EA、EB、EC,电势分别为φA、φB、φC,AB、BC间的电势差分别为UAB、UBC.下列关系中正确的有( )
如图所示,实线为电场线,且AB=BC,电场中的A、B、C三点的场强分别为EA、EB、EC,电势分别为φA、φB、φC,AB、BC间的电势差分别为UAB、UBC.下列关系中正确的有( )| A. | EA>EB>EC | B. | φA>φB>φC | C. | UAB=UBC | D. | UAB<UBC |
 在《验证力的平行四边形定则》实验中,橡皮条的一端固定在木板上,另一端系上两根细绳,细绳的另一端都有绳套.实验中需用两个弹簧测力计分别勾住绳套把橡皮条的一端拉到某一确定的O点.
在《验证力的平行四边形定则》实验中,橡皮条的一端固定在木板上,另一端系上两根细绳,细绳的另一端都有绳套.实验中需用两个弹簧测力计分别勾住绳套把橡皮条的一端拉到某一确定的O点.