题目内容
1. 如图所示,在平面直角坐标系xOy中,x轴上方存在与y轴负方向成45°角的匀强电场,场强大小为E;在x轴下方存在垂直坐标平面向里的匀强磁场,磁感应强度大小为B.现有一质量为m、电荷量为q的质子从y轴正半轴上的P点由静止释放,经电场加速后以速度v0第一次进入磁场,不计质子重力,求:
如图所示,在平面直角坐标系xOy中,x轴上方存在与y轴负方向成45°角的匀强电场,场强大小为E;在x轴下方存在垂直坐标平面向里的匀强磁场,磁感应强度大小为B.现有一质量为m、电荷量为q的质子从y轴正半轴上的P点由静止释放,经电场加速后以速度v0第一次进入磁场,不计质子重力,求:(1)P点的纵坐标;
(2)质子第二次经过x轴时的横坐标.
(3)质子从P点释放到第三次经过x轴所用的时间.
分析 (1)电场力对带电粒子做功,W=qEd,$d=\sqrt{2}y$,
(2)带电粒子在磁场中运动的轨迹是$\frac{1}{4}$圆,$△x=\sqrt{2}r$;
(3)带电粒子第二次进入电场后,沿速度的方向与垂直于速度的方向建立坐标系,带电粒子做类平抛运动.
解答 解:(1)电场力对带电粒子做功等于粒子动能的变化,即:
$qEd=\frac{1}{2}m{v}_{0}^{2}$,
得:$d=\frac{m{v}_{0}^{2}}{2qE}$
又:$d=\sqrt{2}y$,
$d=\sqrt{2}{x}_{1}$
所以:$y=\frac{\sqrt{2}m{v}_{0}^{2}}{4qE}$;
${x}_{1}=\frac{\sqrt{2}m{v}_{0}^{2}}{4qE}$ (2)带电粒子在磁场中运动的轨迹是$\frac{1}{4}$圆,如图,$△x=\sqrt{2}r$;
(2)带电粒子在磁场中运动的轨迹是$\frac{1}{4}$圆,如图,$△x=\sqrt{2}r$;
洛伦兹力提供粒子做圆周运动的向心力,则:$q{v}_{0}B=\frac{m{v}_{0}^{2}}{r}$
得:$△x=\frac{\sqrt{2}m{v}_{0}}{qB}$;
所以:${x}_{2}={x}_{1}+△x=\frac{\sqrt{2}m{v}_{0}^{2}}{4qE}+\frac{\sqrt{2}m{v}_{0}}{qB}$
(3)带电粒子第一次在电场中时:$d=\frac{1}{2}a{t}_{1}^{2}=\frac{qE}{2m}•{t}_{1}^{2}$
解得:${t}_{1}=\frac{m{v}_{0}}{qE}$;
带电粒子在磁场中运动的周期:2πr=v•T,
运动的时间:${t}_{2}=\frac{T}{4}=\frac{πm}{2qB}$
带电粒子第二次进入电场后,沿速度的方向与垂直于速度的方向建立坐标系x′y′,带电粒子做类平抛运动如图.
则:x′=v0t3;
$y′=\frac{1}{2}a{t}_{3}^{2}=\frac{qE}{2m}•{t}_{3}^{2}$;
又:x′=y′;
解得:${t}_{3}=\frac{2m{v}_{0}}{qE}$
质子从P点释放到第三次到达x轴所用的时间:$t={t}_{1}+{t}_{2}+{t}_{3}=\frac{3m{v}_{0}}{qE}+\frac{πm}{2qB}$
答:(1)P点纵坐标y的值$y=\frac{\sqrt{2}m{v}_{0}^{2}}{4qE}$;
(2)质子第二次经过x轴时的横坐标x的值$\frac{\sqrt{2}m{v}_{0}^{2}}{4qE}+\frac{\sqrt{2}m{v}_{0}}{qB}$;
(3)质子从P点释放到第三次到达x轴所用的时间为$\frac{3m{v}_{0}}{qE}+\frac{πm}{2qB}$.
点评 带电粒子的运动分别是匀加速直线运动、匀速圆周运动和类平抛运动,带电粒子第二次进入电场后,沿速度的方向与垂直于速度的方向建立坐标系x′y′来分析粒子的运动是解决该题的关键,要求有较强的分析问题的能力和知识的迁移能力.属于比较难的题目.

 如图所示,等腰直角三角形ABC中存在匀强磁场,比荷相同的两个粒子沿AB方向射入磁场,分别从AC边上的D(AC的中点),C两孔射出,则( )
如图所示,等腰直角三角形ABC中存在匀强磁场,比荷相同的两个粒子沿AB方向射入磁场,分别从AC边上的D(AC的中点),C两孔射出,则( )| A. | 从C,D两孔射出的粒子的运动半径大小之比为RC:RD=2:1 | |
| B. | 从C,D两孔射出的粒子的出射速度大小之比为WC:WD=1:1 | |
| C. | 从C,D两孔射出的粒子在磁场中运动周期之比为TC:TD=2:1 | |
| D. | 从C,D两孔射出的粒子在磁场中的运动时间之比为tC:tD=1:1 |
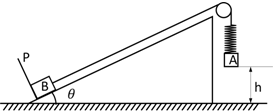 如图所示,固定在水平面上的光滑斜面倾角为30°,物体A、B通过细绳及轻弹簧连接于光滑轻滑轮两侧,P为固定在斜面上且与斜面垂直的光滑挡板,物体A、B的质量分别为m和4m,开始时用手托住物体,滑轮两边的细绳恰好伸直,且左边的细绳与斜面平行,弹簧处于原长状态,A距离地面高度为h时开始下落,在A下落至地面前的瞬间,物体B恰好对挡板无压力.空气阻力不计,下列关于物体A的说法正确的是( )
如图所示,固定在水平面上的光滑斜面倾角为30°,物体A、B通过细绳及轻弹簧连接于光滑轻滑轮两侧,P为固定在斜面上且与斜面垂直的光滑挡板,物体A、B的质量分别为m和4m,开始时用手托住物体,滑轮两边的细绳恰好伸直,且左边的细绳与斜面平行,弹簧处于原长状态,A距离地面高度为h时开始下落,在A下落至地面前的瞬间,物体B恰好对挡板无压力.空气阻力不计,下列关于物体A的说法正确的是( )| A. | 在下落至地面前的过程中机械能守恒 | |
| B. | 在下落至地面前的瞬间速度一定为零 | |
| C. | 在下落至地面前的过程中对轻弹簧做的功为mgh | |
| D. | 在下落至地面前的过程中,可能一直在做加速运动 |
 如图所示为理想变压器原线圈所接正弦交流电源两端的电压-时间图象.原、副线圈匝数比n1:n2=10:1,串联在原线圈电路中交流电流表的示数为1A,则( )
如图所示为理想变压器原线圈所接正弦交流电源两端的电压-时间图象.原、副线圈匝数比n1:n2=10:1,串联在原线圈电路中交流电流表的示数为1A,则( )| A. | 变压器原线圈所接交流电压的有效值为311V | |
| B. | 变压器输出端所接电压表的示数为22$\sqrt{2}$V | |
| C. | 变压器输出端交变电流的频率为50Hz | |
| D. | 变压器的输出功率为220$\sqrt{2}$W |
 如图所示,是街头变压器(可当做理想变压器)通过降压给用户供电的示意图,变压器的输入电压是市区电网的电压,负载变化时输入电压可认为不变.变压器的输出端通过两条输电线连接用户,两条输电线的总电阻用R0表示,变阻器R代表用户用电器的总电阻,当用电器增加时,相当于R减小.下列关于各电表的读数变化说法正确的是( )
如图所示,是街头变压器(可当做理想变压器)通过降压给用户供电的示意图,变压器的输入电压是市区电网的电压,负载变化时输入电压可认为不变.变压器的输出端通过两条输电线连接用户,两条输电线的总电阻用R0表示,变阻器R代表用户用电器的总电阻,当用电器增加时,相当于R减小.下列关于各电表的读数变化说法正确的是( )| A. | 电压表V1读数不变 | B. | 电压表V2读数变大 | ||
| C. | 电流表A1读数变小 | D. | 电流表A2读数变大 |
 已知在t1时刻简谐横波的波形如图实线所示,在t2时刻该波的波形如图虚线所示.t2-t1=0.02s.求:
已知在t1时刻简谐横波的波形如图实线所示,在t2时刻该波的波形如图虚线所示.t2-t1=0.02s.求: 在科学研究中,可以通过在适当的区域施加磁场控制带电粒子的运动.竖直平行正对放置的两金属板A、K间有电压为U的加速电场,S1、S2为A、K板上的两个小孔,且S1和S2在同一水平直线上,如图所示.质量为m、电荷量为q的粒子,从粒子源N右方的小孔S1不断飘入加速电场,其初速度可视为零,然后经过小孔S2垂直于磁场方向进入匀强磁场控制区,粒子经磁场偏转后离开磁场并打在水平放置的感光胶片上,离开磁场时粒子束的等效电流为I,不考虑粒子重力及粒子间的相互作用.
在科学研究中,可以通过在适当的区域施加磁场控制带电粒子的运动.竖直平行正对放置的两金属板A、K间有电压为U的加速电场,S1、S2为A、K板上的两个小孔,且S1和S2在同一水平直线上,如图所示.质量为m、电荷量为q的粒子,从粒子源N右方的小孔S1不断飘入加速电场,其初速度可视为零,然后经过小孔S2垂直于磁场方向进入匀强磁场控制区,粒子经磁场偏转后离开磁场并打在水平放置的感光胶片上,离开磁场时粒子束的等效电流为I,不考虑粒子重力及粒子间的相互作用. (1)在研究平抛运动的实验中,为了正确描绘出小球平抛运动的轨迹,在固定弧形斜槽时,应注意使斜槽末端水平;实验时,每次使小球由静止滚下都应注意从同一高度.
(1)在研究平抛运动的实验中,为了正确描绘出小球平抛运动的轨迹,在固定弧形斜槽时,应注意使斜槽末端水平;实验时,每次使小球由静止滚下都应注意从同一高度.