题目内容
12．A、B两质点分别做匀速圆周运动，其半径之比RA：R B=2：3，角速度之比为ωA：ωB=1：2，则它们的向心加速度之比aA：aB=1：6．分析 根据a=ω2r求解向心加速度之比即可．
解答 解：根据a=ω2r得：
aA：aB=${{ω}_{A}}^{2}{R}_{A}：$${{ω}_{B}}^{2}{R}_{B}=1×2：{2}^{2}×3$=1：6
故答案为：1：6
点评 本题考查匀速圆周运动的描述各物理量之间的关系式，知道a=ω2r，属于简单题目．
练习册系列答案
相关题目
2．
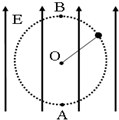如图所示，轻绳系着一带负电、重为G的小球悬挂在竖直向上的匀强电场E中，使小球以悬点O为圆心在竖直平面内做完整的圆周运动，则（ ）
如图所示，轻绳系着一带负电、重为G的小球悬挂在竖直向上的匀强电场E中，使小球以悬点O为圆心在竖直平面内做完整的圆周运动，则（ ）| A． | 小球一定做变速圆周运动 | |
| B． | 小球可能做匀速圆周运动 | |
| C． | 小球经过最低点A时绳子拉力一定最小 | |
| D． | 小球经过最高点B时绳子拉力可能最大 |
3．两个电子以大小不同的初速度沿垂直磁场的方向射入同一匀强磁场中，设r1、r2为这两个电子的运动轨道半径，T1、T2是它们的运动周期，则（ ）
| A． | r1=r2 T1≠T2 | B． | r1≠r2 T1≠T2 | C． | r1=r2 T1=T2 | D． | r1≠r2 T1=T2 |
如图所示，质量m=2kg的小物体P，在方向沿斜面向上，大小F=24N的拉力作用下，从斜面上的A点由静止起沿斜面向上做匀加速运动，物体与斜面间动摩擦因数μ=0.5，斜面的倾角为θ=37°，开始运动后5s末，撤去力F，再过5s，物体P到A点的距离是多少？（g取10m/s2，sin37°=0.6）
7．
如图所示，小钢球以初速度v0在光滑水平面上运动，受到磁铁的侧向作用而沿图示的曲线运动到D点，由此可知（ ）
如图所示，小钢球以初速度v0在光滑水平面上运动，受到磁铁的侧向作用而沿图示的曲线运动到D点，由此可知（ ）| A． | 磁铁在A处 | B． | 磁铁在B处 | C． | 磁铁在C处 | D． | 磁铁在D处 |
17．
如图所示，一列横波沿x轴传播，t0时刻波的图象如图中实线所示．经△t=0.2s，波的图象如图中虚线所示．已知其波长为0.8m，则下述说法中正确的是（ ）
如图所示，一列横波沿x轴传播，t0时刻波的图象如图中实线所示．经△t=0.2s，波的图象如图中虚线所示．已知其波长为0.8m，则下述说法中正确的是（ ）| A． | 若波向右传播，则波的周期可能大于2s | |
| B． | 若波向左传播，则波的周期可能大于0.2s | |
| C． | 若波向左传播，则波的波速可能小于7m/s | |
| D． | 若波速是19m/s，则波向右传播 |
4．
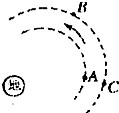三颗人造地球卫星A、B、C在地球的大气层沿如图所示的方向做匀速圆周运动，已知mA=mB＜mC，则三颗卫星（ ）
三颗人造地球卫星A、B、C在地球的大气层沿如图所示的方向做匀速圆周运动，已知mA=mB＜mC，则三颗卫星（ ）| A． | 线速度大小的关系是VA＜VB=VC | |
| B． | 周期关系是TA＞TB=TC | |
| C． | 向心力大小的关系是FA=FB＜FC | |
| D． | 轨道半径和周期的关系是$\frac{{{R}_{A}}^{3}}{{{T}_{A}}^{2}}$=$\frac{{{R}_{B}}^{3}}{{{T}_{B}}^{2}}$=$\frac{{{R}_{C}}^{3}}{{{T}_{C}}^{2}}$ |