题目内容
7. 如图所示,一个正方形导线框abcd,边长为L,质量为m.将线框从距水平匀强磁场上方h处由静止释放,在线框下落过程中,不计空气阻力,线框平面保持在竖直平面内,且cd边始终与水平的磁场边界平行.当ab边刚进入磁场时,线框速度为v.在线框进入磁场的整个过程中,下列说法正确的是( )
如图所示,一个正方形导线框abcd,边长为L,质量为m.将线框从距水平匀强磁场上方h处由静止释放,在线框下落过程中,不计空气阻力,线框平面保持在竖直平面内,且cd边始终与水平的磁场边界平行.当ab边刚进入磁场时,线框速度为v.在线框进入磁场的整个过程中,下列说法正确的是( )| A. | 线框可能做加速度减小的加速运动 | |
| B. | 线框不可能做匀速运动 | |
| C. | 安培力对线框的冲量大小一定为mv | |
| D. | 线框克服安培力做功一定为mg(h+L)-$\frac{1}{2}m{v^2}$ |
分析 当cd边刚进入磁场时,若速度非常大,则cd边受安培力大于线圈重力mg,则线框做加速度逐渐减小的减速运动;
若速度很小,则cd边受安培力小于线圈重力mg,则线框做加速度逐渐减小的加速运动;
根据动量定理计算安培力对线框的冲量大小;
根据动能定理计算线框克服安培力做的功.
解答 解:A、设线框刚进入磁场时速度为v′,则mgh=$\frac{1}{2}$mv′2
E=BLv′,I=$\frac{E}{R}$,安培力F=BIL
联立得:F=$\frac{{B}^{2}{L}^{2}\sqrt{2gh}}{R}$
根据牛顿第二定律:F-mg=ma,
若F>mg,则加速度向上,线框做减速运动,v减小后安培力F减小,则加速度减小,故线框做加速度逐渐减小的减速运动,
若F<mg,根据牛顿第二定律:mg-F=ma
则加速度向下,线框做加速运动,v增大后安培力F增大,则加速度减小,故线框做加速度逐渐减小的加速运动,
若F=mg,则线框做匀速直线运动,故A正确,B错误;
C、根据动量定理:mg△t-I安=mv-mv′,可见安培力的冲量大小与mv不一定相等,故C错误;
D、对全过程根据动能定理:mg(h+L)-W安=$\frac{1}{2}$mv2-0,得:W安=mg(h+L)-$\frac{1}{2}$ mv2.故D正确;
故选:AD.
点评 本题是电磁感应与力学知识的综合,安培力是联系电磁感应和力学的桥梁,安培力的分析和计算以及动能定理的应用是这类问题常用到的工具.

练习册系列答案
相关题目
15. 两根平行的长直金属导轨,其电阻不计,导线ab、cd跨在导轨上且与导轨接触良好,如图所示,ab的电阻大于cd的电阻,当cd在外力F1(大小)的作用下,匀速向右运动时,ab在外力F2(大小)的作用下保持静止,那么在不计摩擦力的情况下(Uab、Ucd是导线与导轨接触间的电势差)( )
两根平行的长直金属导轨,其电阻不计,导线ab、cd跨在导轨上且与导轨接触良好,如图所示,ab的电阻大于cd的电阻,当cd在外力F1(大小)的作用下,匀速向右运动时,ab在外力F2(大小)的作用下保持静止,那么在不计摩擦力的情况下(Uab、Ucd是导线与导轨接触间的电势差)( )
 两根平行的长直金属导轨,其电阻不计,导线ab、cd跨在导轨上且与导轨接触良好,如图所示,ab的电阻大于cd的电阻,当cd在外力F1(大小)的作用下,匀速向右运动时,ab在外力F2(大小)的作用下保持静止,那么在不计摩擦力的情况下(Uab、Ucd是导线与导轨接触间的电势差)( )
两根平行的长直金属导轨,其电阻不计,导线ab、cd跨在导轨上且与导轨接触良好,如图所示,ab的电阻大于cd的电阻,当cd在外力F1(大小)的作用下,匀速向右运动时,ab在外力F2(大小)的作用下保持静止,那么在不计摩擦力的情况下(Uab、Ucd是导线与导轨接触间的电势差)( )| A. | F1>F2 | B. | F1=F2 | C. | Uab>Ucd | D. | Uab=Ucd |
12. 如图所示,用绝缘细线栓一个带负电的小球,带电量大小为q,让它在竖直向下的匀强电场中(场强为E)绕O点做竖直平面内的匀速圆周运动,a、b两点分别是最高点和最低点,不计空气阻力,则下列说法中正确的是( )
如图所示,用绝缘细线栓一个带负电的小球,带电量大小为q,让它在竖直向下的匀强电场中(场强为E)绕O点做竖直平面内的匀速圆周运动,a、b两点分别是最高点和最低点,不计空气阻力,则下列说法中正确的是( )
 如图所示,用绝缘细线栓一个带负电的小球,带电量大小为q,让它在竖直向下的匀强电场中(场强为E)绕O点做竖直平面内的匀速圆周运动,a、b两点分别是最高点和最低点,不计空气阻力,则下列说法中正确的是( )
如图所示,用绝缘细线栓一个带负电的小球,带电量大小为q,让它在竖直向下的匀强电场中(场强为E)绕O点做竖直平面内的匀速圆周运动,a、b两点分别是最高点和最低点,不计空气阻力,则下列说法中正确的是( )| A. | 小球在运动中机械能守恒 | B. | 小球经过a点时,机械能最大 | ||
| C. | 小球质量为$\frac{Eq}{g}$ | D. | 小球经过a点时,电势能最大 |

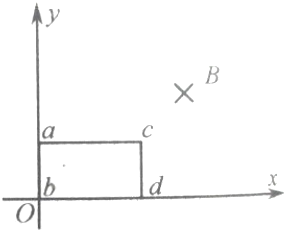 如图所示,在光滑水平面上,有一坐标系xOy,其第一象限内充满着垂直平面坐标向里的磁场,磁感应强度B沿y方向不变,沿x方向的变化满足B=B0+kx(T),有一长ac=l1,宽cd=l2的矩形线框abcd,其总电阻为R,初始时两边正好和xy轴重合.求:
如图所示,在光滑水平面上,有一坐标系xOy,其第一象限内充满着垂直平面坐标向里的磁场,磁感应强度B沿y方向不变,沿x方向的变化满足B=B0+kx(T),有一长ac=l1,宽cd=l2的矩形线框abcd,其总电阻为R,初始时两边正好和xy轴重合.求: 如图所示,MN、PQ为相距L=0.5m的光滑平行导轨,导轨平面与水平面夹角为θ=37°,导轨处于磁感应强度为B=1T、方向垂直于导轨平面向上的匀强磁场中,在两导轨的M、P两端接有一电阻为R=2Ω的定值电阻,回路其余电阻不计.一质量为m=0.2kg的导体棒垂直导轨放置且与导轨接触良好.今平行于导轨对导体棒施加一作用力F,使导体棒从ab位置由静止开始沿导轨向下匀加速滑到底端,滑动过程中导体棒始终垂直于导轨,加速度大小为a=4m/s2,经时间t=1s滑到cd位置,从ab到cd过程中电阻发热为Q=0.25J.求:
如图所示,MN、PQ为相距L=0.5m的光滑平行导轨,导轨平面与水平面夹角为θ=37°,导轨处于磁感应强度为B=1T、方向垂直于导轨平面向上的匀强磁场中,在两导轨的M、P两端接有一电阻为R=2Ω的定值电阻,回路其余电阻不计.一质量为m=0.2kg的导体棒垂直导轨放置且与导轨接触良好.今平行于导轨对导体棒施加一作用力F,使导体棒从ab位置由静止开始沿导轨向下匀加速滑到底端,滑动过程中导体棒始终垂直于导轨,加速度大小为a=4m/s2,经时间t=1s滑到cd位置,从ab到cd过程中电阻发热为Q=0.25J.求: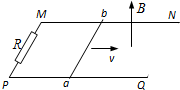 如图所示,水平面上有两根相距0.5m的足够长的光滑平行金属导轨MN和PQ,它们的电阻可忽略不计,在M和P之间接有阻值R=4Ω的电阻.导体棒ab长L=0.5m,其电阻为r=1Ω,质量m=0.1kg,与导轨接触良好.整个装置处于方向竖直向上的匀强磁场中,磁感应强度B=0.4T.现在在导体棒ab上施加一个水平向右的力F,使ab以v=10m/s的速度向右做匀速运动时,求:
如图所示,水平面上有两根相距0.5m的足够长的光滑平行金属导轨MN和PQ,它们的电阻可忽略不计,在M和P之间接有阻值R=4Ω的电阻.导体棒ab长L=0.5m,其电阻为r=1Ω,质量m=0.1kg,与导轨接触良好.整个装置处于方向竖直向上的匀强磁场中,磁感应强度B=0.4T.现在在导体棒ab上施加一个水平向右的力F,使ab以v=10m/s的速度向右做匀速运动时,求: 如图所示,空间中存在着竖直向上的匀强电场,现有一带负电的粒子,电荷量为q,质量为m,从M点以初速度v0水平飞入电场,最后打到倾角为θ的挡板上的某点N,不计粒子重力,求:
如图所示,空间中存在着竖直向上的匀强电场,现有一带负电的粒子,电荷量为q,质量为m,从M点以初速度v0水平飞入电场,最后打到倾角为θ的挡板上的某点N,不计粒子重力,求: 如图所示,在范围很大的水平向右的匀强电场中,一个电荷量为-q的油滴,从A点以速度v竖直向上射入电场.已知油滴质量为m,重力加速度为g,当油滴到达运动轨迹的最高点时,测得它的速度大小恰为$\frac{v}{2}$.问:
如图所示,在范围很大的水平向右的匀强电场中,一个电荷量为-q的油滴,从A点以速度v竖直向上射入电场.已知油滴质量为m,重力加速度为g,当油滴到达运动轨迹的最高点时,测得它的速度大小恰为$\frac{v}{2}$.问: