题目内容
10. 如图所示,光滑的平行导轨间距为L,倾角为θ,处在磁感应强度为B的匀强磁场中,导轨中接入电动势为E,内阻为r的直流电源,电路中其余电阻不计,将质量为m电阻为R的导体棒由静止释放,求:导体棒在释放瞬间的加速度.
如图所示,光滑的平行导轨间距为L,倾角为θ,处在磁感应强度为B的匀强磁场中,导轨中接入电动势为E,内阻为r的直流电源,电路中其余电阻不计,将质量为m电阻为R的导体棒由静止释放,求:导体棒在释放瞬间的加速度.
分析 导体棒在释放瞬间受重力、支持力和安培力,根据正交分解求出导体棒所受的合力,根据牛顿第二定律求出释放瞬间的加速度
解答  解:受力分析如图所示,导体棒受重力mg、支持力FN和安培力F,由牛顿第二定律:
解:受力分析如图所示,导体棒受重力mg、支持力FN和安培力F,由牛顿第二定律:
mgsin θ-Fcos θ=ma①
F=BIL②
I=$\frac{E}{R+r}$③
由①②③式可得
a=gsin θ-$\frac{BELcosθ}{m(R+r)}$.
答:导体棒在释放瞬间的加速度的大小为gsin θ-$\frac{BELcosθ}{m(R+r)}$.
点评 解决本题的关键能够正确地进行受力分析,求出合力,运用牛顿第二定律进行求解.

练习册系列答案
相关题目
15. 阻值不计的矩形线圈在匀强磁场中,绕垂直于磁感线的轴匀速转动,线圈两端的电压随时间的变化规律如图所示.则下列说法中正确的是( )
阻值不计的矩形线圈在匀强磁场中,绕垂直于磁感线的轴匀速转动,线圈两端的电压随时间的变化规律如图所示.则下列说法中正确的是( )
 阻值不计的矩形线圈在匀强磁场中,绕垂直于磁感线的轴匀速转动,线圈两端的电压随时间的变化规律如图所示.则下列说法中正确的是( )
阻值不计的矩形线圈在匀强磁场中,绕垂直于磁感线的轴匀速转动,线圈两端的电压随时间的变化规律如图所示.则下列说法中正确的是( )| A. | 线圈两端电压的平均值为10V | |
| B. | 电压表连接在线圈两端时,其示数为20V | |
| C. | 在0.01s时,线圈平面与磁场垂直 | |
| D. | 当接外电路时,线圈内的电流方向1s内改变100次 |
20. 电火花塞是一种常用的点火装置,它在高压时会产生电火花.但为电火花塞供电的一般都是低压直流电源,因此要使用如图所示的装置来实现点火.其中,变压器的初级线圈通过触点开关与低压直流电源相连,次级线圈接在电火花塞的两端.触点开关能利用金属触点可以使电路持续的通断,从而在次级线圈上产生5000V以上的电压,这样就能在火花塞上产生火花.关于该点火装置的分析,以下说法正确的是( )
电火花塞是一种常用的点火装置,它在高压时会产生电火花.但为电火花塞供电的一般都是低压直流电源,因此要使用如图所示的装置来实现点火.其中,变压器的初级线圈通过触点开关与低压直流电源相连,次级线圈接在电火花塞的两端.触点开关能利用金属触点可以使电路持续的通断,从而在次级线圈上产生5000V以上的电压,这样就能在火花塞上产生火花.关于该点火装置的分析,以下说法正确的是( )
 电火花塞是一种常用的点火装置,它在高压时会产生电火花.但为电火花塞供电的一般都是低压直流电源,因此要使用如图所示的装置来实现点火.其中,变压器的初级线圈通过触点开关与低压直流电源相连,次级线圈接在电火花塞的两端.触点开关能利用金属触点可以使电路持续的通断,从而在次级线圈上产生5000V以上的电压,这样就能在火花塞上产生火花.关于该点火装置的分析,以下说法正确的是( )
电火花塞是一种常用的点火装置,它在高压时会产生电火花.但为电火花塞供电的一般都是低压直流电源,因此要使用如图所示的装置来实现点火.其中,变压器的初级线圈通过触点开关与低压直流电源相连,次级线圈接在电火花塞的两端.触点开关能利用金属触点可以使电路持续的通断,从而在次级线圈上产生5000V以上的电压,这样就能在火花塞上产生火花.关于该点火装置的分析,以下说法正确的是( )| A. | 该装置说明变压器也能改变恒定电流的电压 | |
| B. | 点火装置中变压器的次级线圈匝数应大于初级线圈的匝数 | |
| C. | 为使次级线圈的两端产生高压,触点开关应始终闭合 | |
| D. | 为使该点火装置一直保持在正常工作状态,触点开关应始终闭合 |

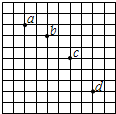 在做研究平抛运动的实验时,让小球多次沿同一轨道运动,通过描点法画出小球平抛运动的轨迹.
在做研究平抛运动的实验时,让小球多次沿同一轨道运动,通过描点法画出小球平抛运动的轨迹.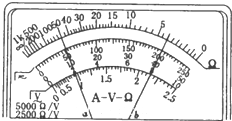 多用电表是生活实际中常用的仪器,某同学使用多用电表进行了两次测量,指针所指的位置分别如图中a、b所示.若选择开关处在“×10”的欧姆挡时指针位于a,则被测电阻的阻值是500Ω;若选择开关处在“直流电压2.5V”挡时,指针位于b,则被测电压是2.0V.
多用电表是生活实际中常用的仪器,某同学使用多用电表进行了两次测量,指针所指的位置分别如图中a、b所示.若选择开关处在“×10”的欧姆挡时指针位于a,则被测电阻的阻值是500Ω;若选择开关处在“直流电压2.5V”挡时,指针位于b,则被测电压是2.0V. 如图所示,正方形金属线圈处在磁感应强度B=0.4T的匀强磁场区域内,磁场的方向与线圈平面垂直.金属线圈所围的面积S=100cm2,匝数n=100,线圈电阻r=1.0Ω.线圈与电阻R构成闭合回路,电阻的阻值R=3.0Ω,当线圈从图示位置开始绕中心轴OO′按顺时针方向以角速度ω=2rad/s匀速转动时,求:
如图所示,正方形金属线圈处在磁感应强度B=0.4T的匀强磁场区域内,磁场的方向与线圈平面垂直.金属线圈所围的面积S=100cm2,匝数n=100,线圈电阻r=1.0Ω.线圈与电阻R构成闭合回路,电阻的阻值R=3.0Ω,当线圈从图示位置开始绕中心轴OO′按顺时针方向以角速度ω=2rad/s匀速转动时,求: