题目内容
16.一颗人造卫星在某行星上空绕行星做匀速圆周运动,经过时间t,卫星运动的弧长为s,卫星与行星的中心连线扫过的角度为α,万有引力常量为G.则卫星的环绕周期T=$\frac{2πt}{α}$,该行星的质量M=$\frac{{s}_{\;}^{3}}{αG{t}_{\;}^{2}}$.分析 根据角速度的定义式求出角速度,根据角速度与周期间的关系求出周期,万有引力提供向心力,由万有引力公式与牛顿第二定律求出行星的质量.
解答 解:根据角速度的定义$ω=\frac{α}{t}$,卫星的环绕周期$T=\frac{2π}{ω}=\frac{2π}{\frac{α}{t}}=\frac{2πt}{α}$
根据线速度的定义$v=\frac{s}{t}$
轨道半径$r=\frac{v}{ω}=\frac{s}{α}$
卫星绕行星做匀速圆周运动,万有引力提供向心力
$G\frac{Mm}{{r}_{\;}^{2}}=m{ω}_{\;}^{2}r$
行星的质量$M=\frac{{ω}_{\;}^{2}{r}_{\;}^{3}}{G}=\frac{(\frac{α}{t})_{\;}^{2}(\frac{s}{α})_{\;}^{3}}{G}=\frac{{s}_{\;}^{3}}{αG{t}_{\;}^{2}}$
故答案为:$\frac{2πt}{α}$ $\frac{{s}_{\;}^{3}}{αG{t}_{\;}^{2}}$
点评 本题考查了万有引力定律的应用,掌握描述圆周运动的各物理量的定义、各量间的关系,应用牛顿第二定律可以解题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.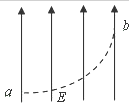 一带电油滴在匀强电场E中的运动轨迹如图中虚线所示,电场方向竖直直向下.若不计空气阻力,则此带电油滴从a运动到b的过程中,下列说法正确的是( )
一带电油滴在匀强电场E中的运动轨迹如图中虚线所示,电场方向竖直直向下.若不计空气阻力,则此带电油滴从a运动到b的过程中,下列说法正确的是( )
 一带电油滴在匀强电场E中的运动轨迹如图中虚线所示,电场方向竖直直向下.若不计空气阻力,则此带电油滴从a运动到b的过程中,下列说法正确的是( )
一带电油滴在匀强电场E中的运动轨迹如图中虚线所示,电场方向竖直直向下.若不计空气阻力,则此带电油滴从a运动到b的过程中,下列说法正确的是( )| A. | 油滴带正电 | B. | 电势能增加 | ||
| C. | 动能增加 | D. | 重力势能和电势能之和增加 |
11.有关物理学史的描述,下列说法中正确的是( )
| A. | 伽利略通过实验证实了力是维持物体运动的原因 | |
| B. | 卢瑟福最早发现了原子核的裂变 | |
| C. | 安培最早发现磁场对电流可以产生力的作用 | |
| D. | 奥斯特最早研究电磁感应现象,并发现感应电动势与磁通量变化率成正比 |

 如图所示,MNPQ在同一竖直平面内,其中,MP段在水平地面上,PQ为半径为R内壁光滑的半圆轨道,O为圆心,POQ为竖直的直径.N是MP间的一点,NP段粗糙,长为L.可视为质点的小物块A,与NP间的动摩擦因数为μ.A自N点开始以水平初速度v0沿NP方向运动,重力加速度为g.
如图所示,MNPQ在同一竖直平面内,其中,MP段在水平地面上,PQ为半径为R内壁光滑的半圆轨道,O为圆心,POQ为竖直的直径.N是MP间的一点,NP段粗糙,长为L.可视为质点的小物块A,与NP间的动摩擦因数为μ.A自N点开始以水平初速度v0沿NP方向运动,重力加速度为g. 如图所示,竖直平面内有四分之一圆弧轨道固定在水平桌面上,轨道下端与水平桌面相切,圆心为O点,A点和B点分别是圆弧轨道的最高点和最低点.一小滑块自圆弧轨道A点无初速释放,在B点沿水平方向飞出,落到水平地面C点.已知圆弧轨道光滑,半径R=0.2m;小滑块的质量m=1.0kg,B点到水平地面的高度h=0.8m,取重力加速度g=10m/s2.求:
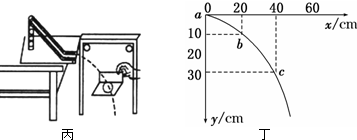
如图所示,竖直平面内有四分之一圆弧轨道固定在水平桌面上,轨道下端与水平桌面相切,圆心为O点,A点和B点分别是圆弧轨道的最高点和最低点.一小滑块自圆弧轨道A点无初速释放,在B点沿水平方向飞出,落到水平地面C点.已知圆弧轨道光滑,半径R=0.2m;小滑块的质量m=1.0kg,B点到水平地面的高度h=0.8m,取重力加速度g=10m/s2.求: 在“研究平抛物体的运动”的实验中
在“研究平抛物体的运动”的实验中