题目内容
14.质量为M,长为L的船静止在静水中,船头及船尾各站着质量分别为m1及m2的人,当两人互换位置后,船的位移有多大.分析 人和小船组成的系统动量守恒,根据动量守恒定律求出船移动的位移大小.
解答 解:若让其中的一个人先从船头走到船尾,船和人组成的系统,在水平方向上动量守恒,人在船上行进,船向后退,规定人速度方向为正方向,由动量守恒定律得:
m1v-(M+m2)V=0.
人从船头走到船尾,设船向前的距离为x1,则人相对于地面的距离为L-x1;由于所有的时刻二者的速度大小关系不变,则:m1vt-(M+m2)Vt=0.
即:m1$\frac{L-{x}_{1}}{t}$-(M+m2)$\frac{{x}_{1}}{t}$=0,
解得:x1=$\frac{{m}_{1}L}{M+{m}_{1}+{m}_{2}}$;
同理.另一个人从船尾走到船头时,船向后的位移:${x}_{2}=\frac{{m}_{2}L}{M+{m}_{1}+{m}_{2}}$
所以船的总位移:x=x1-x2=$\frac{({m}_{1}-{m}_{2})L}{M+{m}_{1}+{m}_{2}}$
答:船的位移是$\frac{({m}_{1}-{m}_{2})L}{M+{m}_{1}+{m}_{2}}$.
点评 解决本题的关键掌握动量守恒定律的条件,以及知道在运用动量守恒定律时,速度必须相对于地面为参考系.

练习册系列答案
相关题目
5. 趣味运动会上运动员手持网球拍托球沿水平面匀加速跑,设球拍和球的质量分别为M、m,球拍平面和水平面之间的夹角为θ,球拍与球保持相对静止,它们间摩擦及空气阻力不计,则( )
趣味运动会上运动员手持网球拍托球沿水平面匀加速跑,设球拍和球的质量分别为M、m,球拍平面和水平面之间的夹角为θ,球拍与球保持相对静止,它们间摩擦及空气阻力不计,则( )
 趣味运动会上运动员手持网球拍托球沿水平面匀加速跑,设球拍和球的质量分别为M、m,球拍平面和水平面之间的夹角为θ,球拍与球保持相对静止,它们间摩擦及空气阻力不计,则( )
趣味运动会上运动员手持网球拍托球沿水平面匀加速跑,设球拍和球的质量分别为M、m,球拍平面和水平面之间的夹角为θ,球拍与球保持相对静止,它们间摩擦及空气阻力不计,则( )| A. | 运动员的加速度为gtanθ | |
| B. | 球拍对球的作用力为$\frac{mg}{sinθ}$ | |
| C. | 运动员对球拍的作用力为$\frac{Mg}{cosθ}$ | |
| D. | 若加速度大于gsinθ,球一定沿球拍向上运动 |
2. 图甲是电场中一条电场线,A,B是电场线上的两点,一带正电粒子(只受电场力)沿直线从A点运动到B点的v-t图象如图乙所示,则关于A,B两点的电场强度EA和EB的下列说法正确的是( )
图甲是电场中一条电场线,A,B是电场线上的两点,一带正电粒子(只受电场力)沿直线从A点运动到B点的v-t图象如图乙所示,则关于A,B两点的电场强度EA和EB的下列说法正确的是( )
 图甲是电场中一条电场线,A,B是电场线上的两点,一带正电粒子(只受电场力)沿直线从A点运动到B点的v-t图象如图乙所示,则关于A,B两点的电场强度EA和EB的下列说法正确的是( )
图甲是电场中一条电场线,A,B是电场线上的两点,一带正电粒子(只受电场力)沿直线从A点运动到B点的v-t图象如图乙所示,则关于A,B两点的电场强度EA和EB的下列说法正确的是( )| A. | 该电场一定是匀强电场 | |
| B. | EA<EB,电场方向从A向B | |
| C. | EA>EB,电场方向从A向B | |
| D. | 若该电场是由点电荷产生,在点电荷一定在B点的右方 |
19. 如图所示,用细线拴着质量为m的小球,绕O点在竖直面内做半径为R的变速圆周运动,P和Q点分别为轨迹最高点和最低点,小球到达这两点的速度大小分别是vP和vQ,向心加速度大小分别为aP和aQ,绳子受到的拉力大小分别为FP和FQ,下列判断正确的是( )
如图所示,用细线拴着质量为m的小球,绕O点在竖直面内做半径为R的变速圆周运动,P和Q点分别为轨迹最高点和最低点,小球到达这两点的速度大小分别是vP和vQ,向心加速度大小分别为aP和aQ,绳子受到的拉力大小分别为FP和FQ,下列判断正确的是( )
 如图所示,用细线拴着质量为m的小球,绕O点在竖直面内做半径为R的变速圆周运动,P和Q点分别为轨迹最高点和最低点,小球到达这两点的速度大小分别是vP和vQ,向心加速度大小分别为aP和aQ,绳子受到的拉力大小分别为FP和FQ,下列判断正确的是( )
如图所示,用细线拴着质量为m的小球,绕O点在竖直面内做半径为R的变速圆周运动,P和Q点分别为轨迹最高点和最低点,小球到达这两点的速度大小分别是vP和vQ,向心加速度大小分别为aP和aQ,绳子受到的拉力大小分别为FP和FQ,下列判断正确的是( )| A. | vQ2-vP2=2gR | B. | aQ-aP=3g | C. | FQ-FP=6mg | D. | vQ-vP=$\sqrt{gR}$ |
6. 如图所示,一个质量为M木箱原来静止在光滑水平面上,木箱内粗糙的底板上放着一个质量为m的小木块,m=0.25M,现使木箱获得一个向右的初速度v0,则( )
如图所示,一个质量为M木箱原来静止在光滑水平面上,木箱内粗糙的底板上放着一个质量为m的小木块,m=0.25M,现使木箱获得一个向右的初速度v0,则( )
 如图所示,一个质量为M木箱原来静止在光滑水平面上,木箱内粗糙的底板上放着一个质量为m的小木块,m=0.25M,现使木箱获得一个向右的初速度v0,则( )
如图所示,一个质量为M木箱原来静止在光滑水平面上,木箱内粗糙的底板上放着一个质量为m的小木块,m=0.25M,现使木箱获得一个向右的初速度v0,则( )| A. | 木箱运动和小木块最终都静止 | |
| B. | 小木块最终速度大小为4v0,方向向右 | |
| C. | 木箱最终速度大小为0.8v0,方向向右 | |
| D. | 如果小木块与木箱的左壁碰撞后相对木箱静止,则二者将一起向左运动 |
 “魔盘”是一种神奇的游乐设施,它是一个能绕中心轴转动的带有竖直侧壁的大型转盘,随着“魔盘”转动角速度的增大,“魔盘”上的人可能滑向盘的边缘.如图所示,质量为m的人(视为质点)坐在转盘上,与转盘中心O相距r,转盘的半径为R,人与盘面及侧壁间的动摩擦因数均为μ,设最大静摩擦力等于滑动摩擦力,重力加速度为g.
“魔盘”是一种神奇的游乐设施,它是一个能绕中心轴转动的带有竖直侧壁的大型转盘,随着“魔盘”转动角速度的增大,“魔盘”上的人可能滑向盘的边缘.如图所示,质量为m的人(视为质点)坐在转盘上,与转盘中心O相距r,转盘的半径为R,人与盘面及侧壁间的动摩擦因数均为μ,设最大静摩擦力等于滑动摩擦力,重力加速度为g.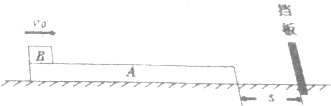
 如图所示,一轻质薄木板静止在粗糙水平桌面,左端通过细绳跨过桌子边缘的定滑轮与重物相连,用手托住重物,细绳处于伸直状态.木板上有一质量为m=1kg的小铁块,它离木板的右端距离为L=0.5m,铁块与木板、木板与桌面间动摩擦因数为μ=0.1.释放重物,从静止开始以a0=2m/s2的加速度将木板从铁块下抽出,假设铁块大小、滑轮摩擦不计,桌面足够长,g取10m/s2,求:
如图所示,一轻质薄木板静止在粗糙水平桌面,左端通过细绳跨过桌子边缘的定滑轮与重物相连,用手托住重物,细绳处于伸直状态.木板上有一质量为m=1kg的小铁块,它离木板的右端距离为L=0.5m,铁块与木板、木板与桌面间动摩擦因数为μ=0.1.释放重物,从静止开始以a0=2m/s2的加速度将木板从铁块下抽出,假设铁块大小、滑轮摩擦不计,桌面足够长,g取10m/s2,求: 如图所示的传动装置中,B、C两轮固定在一起绕同一轴转动,A、B两轮用皮带传动,三轮半径关系是rA=rC=2rB.则:
如图所示的传动装置中,B、C两轮固定在一起绕同一轴转动,A、B两轮用皮带传动,三轮半径关系是rA=rC=2rB.则: